Dowodzenie twierdzeń - czworokąty wpisane w okrąg lemurek: Witam! Jak zwykle cały mam problem Nie potrafię zrobić 3 zadanek z dowodzenia twierdzeń jakie mi zostały. Bardzo liczę na waszą pomoc 1) W czworokącie ABCD wpisanym w okrąg przedłużamy boki AB i CD aż do przecieęcia w punkcie E. Wykaż, że dwusieczna kąta AED jest równoległa do dwusiecznej kąta CSB, gdzie S jest punktem przecięcia przekątnych czworokąta ABCD. 2) Trójkąt ABC wpisano w okrąg, następnie poprowadzono sieczną równoległą do stycznej w punkcie A, przecinającą boki AC i AB odpowiednio w punktach D i E. Udowodnij, że na czworokącie BCED można opisać okrąg. 3) W czworokącie wpisanym w okrąg prowadzimy dwusieczne dwóch przeciwległych kątów, przecinające okrąg w punktach E, F. Wykaż, że odcinek EF jest średnicą tego okręgu.

think: Godzio przecież to zadania stworzone dla Ciebie, nie rozumiem, czemu ich jeszcze nie roztrzaskałeś

Godzio: Już się nad nimi namęczyłem i nic z tego nie wyszło chodź będę próbować

think: no to, że mi nic nie wyszło, to mnie średnio zdziwiło, ale że Tobie...

Godzio: no wiem wiem ale nie przepadam za tego typu dowodami, ale widzę że Cię to kusi to możesz zrobić to się chociaż czegoś nauczę

think: no przecież napisałam, że mi też się nie udało zresztą zostałam dzisiaj poczęstowana piwkiem i wolę się nie kompromitować

Godzio: nie odczytałem poprawnie Twojej odpowiedzi sie jeszcze pomysli

think: Kometo może Ty nas oświecisz

Godzio: tak mi się wydaje że 3 jest banalne

think: a mi się dziś nic nie wydaje, zafundowałam sobie podróż 'sentymentalną' po utworach muzycznych dla mnie szczególnych

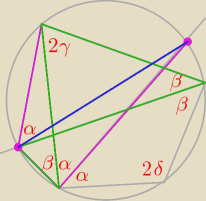
Godzio: zad. 3 Ufff Udało się, 2α + 2β = 180 α + β = 90 Dowód jest oparty na kątach opartych na tym samym łuku

think: no Godzio jeszcze tylko dwa i będzie po ptakach

kometa:

think: co za wstawiony wieczorek... mi już przechodzi, ale i ja słabszym specyfikiem się raczyłam

Godzio: Nie da się tych zadań zrobić normalnymi sposobami

think: to zrób nienormalnym jeśli takowy znasz

Eta: Godzio Skorzystaj z własności punktów leżących na dwusiecznej .......

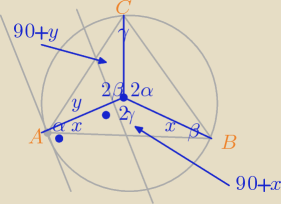
Godzio: x + y = α zał. 90 + y + β = 180, 90 + x + γ = 180 y + β = 90, x + γ = 90 ⇒ y + β = x + γ 2γ + 2x = 180 x + γ = 90, c.n.d Nie jestem pewien czy to poprawne dlatego sprawdźcie proszę

Godzio: Dobra to teraz to pierwsze, tylko że z tego co się orientuje to pierwsze słyszę o "własności punktów leżących na dwusiecznej" ale spokojnie najpierw rysunek sobie zrobię

Eta: Punkty leżące na dwusiecznej są równo oddalone od ramion kąta

Godzio: Nie wymyślę chyba

Eta: Gustlik Roztrzaskaj zad. 1) ....... swoim najprostszym sposobem

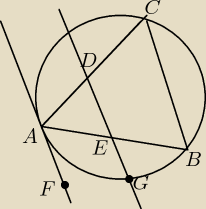
full wypas: Zadanie 2. Aby wykazać tezę wystarczy pokazać tylko, że ∡DCB + ∡DEB =180. Niech zatem α=∡ACB. Wówczas także ∡BAF=α na mocy twierdzenia o kącie dopisanym. Teraz wystarczy zauważyć, że skoro styczna w punkcie A i sieczna są równoległe to ∡BEG=∡BAF=α to ∡BEF=180−α, co w połączeniu z ∡ACB=α daje tezę. PZDR

full wypas: Mała literówka na górze. Poprawnie : Zadanie 2. Aby wykazać tezę wystarczy pokazać tylko, że ∡DCB + ∡DEB =180. Niech zatem α=∡ACB. Wówczas także ∡BAF=α na mocy twierdzenia o kącie dopisanym. Teraz wystarczy zauważyć, że skoro styczna w punkcie A i sieczna są równoległe to ∡BEG=∡BAF=α to ∡BED=180−α, co w połączeniu z ∡ACB=α daje tezę.

Eta:

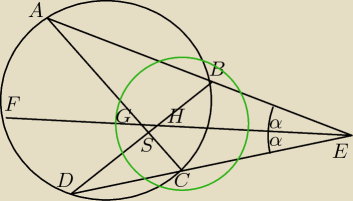
full wypas: Zad 1 Ponieważ kąty ABD i ACD są oparte na tym samym łuku to miary ich kątów są równe, z tego wnioskujemy, że miary kątów EBD i ECA także są równe(są to kąty przyległe do wcześniej wspomnianych). Łącząc tą zależność z ∡AEF = ∡FED = α otrzymamy, że ∡BHE=∡CGE, gdyż trójkąty EBH i ECG są podobne− cecha kkk. Niech zatem ∡BHE= 2β , wtedy także ∡EGC=2β....

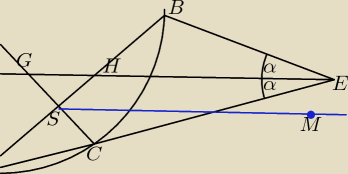
full wypas: Kontynuacja zad 1... Zauważmy teraz, że ∡GHS = 2β (jako kąt wierzchołkowy z kątem BHE=2β), z poprzedniego mamy także ∡HGS=∡EGC =2β. Z tego wnioskujemy, że ∡HSC=4β. Dwusieczna kąta HSC dzieli kąt na połowy, więc otrzymujemy ∡CSM=∡MSH= 2β co w połączeniu z ∡BHE = 2β pokazuje równoległość odcinków HE i SM i stanowi tezę. Niepotrzebnie wprowadziłem oznaczenie 2β, wystarczyło tylko β. Wybaczcie za utrudnienie

Godzio: eleganckie rozwiązanie

Eta: Nawet bardziej niż "eleganckie" Można śmiało powiedzieć,że wypasione na full

Ania: Przepraszam, a może ktoś opisać czemu w zadaniu 3 dowód oparty jest na kątach opartych na tym samym łuku?

mieszko: skąt wziołeś nagle 4 beta jest taka właściwość ?

s:

JA: odpowiedz dla mieszka: ∡GSH = 180−4β więc ∡HSC = 180 − (180−4β) ∡HSC = 180 −180 + 4β ∡HSC = 4β