Obliczyć objętość prostopadłościanu
Ola: Przekątna prostopadłościanu ma długość 6√3 i jest nachylona do płaszczyzny
podstawy pod kątem 30° . Oblicz objętość tego prostopadłościanu ,
wiedząc że jedno z krawędzi jego podstawy ma długośc 6 cm
9 gru 18:02
9 gru 18:07
Ola: Widziałam to zadanie ale nierozumie jego rozwiązania . Jak by ktoś mógł mi wytłumaczyć jak
chłop krowie na miedzy ?
9 gru 18:53
a7: 1. mamy prostopadłościan
2.przekątna prostopadłościanu łączy górę z dołem po ukosie, (ale nie po ścianach bocznych)
3. kąt nachylenia przekątnej do płaszczyzny podstawy to kąt między tą przekątną a przekątną
podstawy
4.bierzemy sinus trzydziestu stopni (czyli jedna druga 1/2) a ten sinus to wysokość
prostopadłościanu do przekątnej równej 6√3
wychodzi nam H=...
5. liczymy z tw. Pitagorasa dla ΔAA1C przekątną podstawy d i wychodzi nam 9
6.liczymy z tw. Pitagorasa dla ΔABC drugi bok podstawy i wychodzi nam 3√5
7. liczymy objętość V=6*3√5*9=......
daj znać, który punkt jeszcze ew. uszczegółowić....
9 gru 19:03
Ola: w 7 punkcie będzie 54√15
9 gru 19:16
a7: tak w punkcie 7. 6*3√5*3√3 H (wysokość) jest równa 3√3 a nie jak 19:03 napisałam 9
czyli owszem wychodzi 54√15
9 gru 19:31
Ola: Tej 9 z twierdzenia tw. Pitagorasa nie mogę obliczyć
a2+b2=c2
9 gru 19:34
a7:
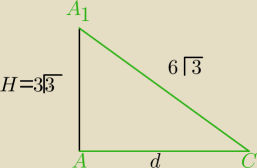
d
2+H
2=(6
√3)
2
d
2=(6
√3)
2−H
2
d
2=(6
√3)
2−(3
√32
d
2=36*3−9*3=81
d=
√81=9
========
9 gru 19:39
Ola: dzięki
9 gru 19:43
a@b:
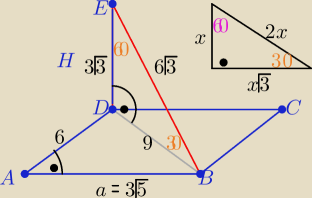
Krótko i na temat

( bez sinusów
Z trójkąta "ekierkowego" o kątach ostrych 30
o,60
o
|DE|=H=3
√3 to |DB|= 3
√3*
√3= 9
Z tw. Pitagorasa w ΔABD:
a
2=9
2−6
2 ⇒ a=
√45=3
√5
V= 6*3
√5*3
√3 = 54
√15
====================
i po ptokach

9 gru 23:12
a7: 
9 gru 23:13
 d2+H2=(6√3)2
d2=(6√3)2−H2
d2=(6√3)2−(3√32
d2=36*3−9*3=81
d=√81=9
========
d2+H2=(6√3)2
d2=(6√3)2−H2
d2=(6√3)2−(3√32
d2=36*3−9*3=81
d=√81=9
========
 Krótko i na temat
Krótko i na temat  ( bez sinusów
Z trójkąta "ekierkowego" o kątach ostrych 30o,60o
|DE|=H=3√3 to |DB|= 3√3*√3= 9
Z tw. Pitagorasa w ΔABD:
a2=92−62 ⇒ a=√45=3√5
V= 6*3√5*3√3 = 54√15
====================
i po ptokach
( bez sinusów
Z trójkąta "ekierkowego" o kątach ostrych 30o,60o
|DE|=H=3√3 to |DB|= 3√3*√3= 9
Z tw. Pitagorasa w ΔABD:
a2=92−62 ⇒ a=√45=3√5
V= 6*3√5*3√3 = 54√15
====================
i po ptokach

