Wartości funkcji trygonometrycznych. Kokosimek: 1. Oblicz wartości pozostałych funkcji trygonometrcznych, jeżeli wiadomo, że: ctga= 2 oraz a E (180 270) 2. Uzasadnij, że dla każdego kąta a prawdziwa jest równość: (sina+cosa)²+(sina−cosa)²=2

a7: 2. sin²a+2sinacosa+cos²a+sin²−2sinacosa+cos²a=2sin²a+2cos²a=2(sin²a+cos²a)=2*1=2

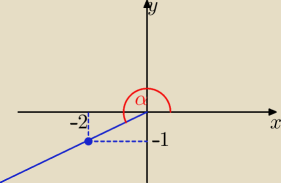
a@b: III ćw ctgα=2 , tgα=1/2 x=−2, y= −1 r=√x²+y²= √5 sinα=y/r=... cosα=x/r=....

a7: a∊ trzecia ćwiartka czyli sina<0 cos<a<0 tga>0 tga=1/ctga=1/2 w linku są tożsamości trygonometryczne https://matematykaszkolna.pl/strona/1722.html

	√5
sin2a=tga/(tga+ctga)=1/2 : (5/2)=1/5 sina=−		cosa liczymy z jedynki
	5

trygonometrycznej pamiętając, że jest ujemny w trzeciej ćwiartce.

salamandra: 1. ctgα = 2, przedział od 180 do 270, oznacza, że jesteśmy w ćwiartce III.

	x
ctg =		, czyli x = −2, y= −1
	y

r= √(−2)²+(−1)² = √5

	y		−1		−√5
sinα =		, więc		=
	r		√5		5

	x		−2		−2√5
cos α =		, więc		=
	r		√5		5

	−1		1
tg α =		=
	−2		2

2. (sinα+cosα)² + (sinα−cosα)² = 2 sin²α+2sinαcosα+cos²α + sin²α−2sinαcosα + cos²α = =sin²α + cos²α + sin²α + cos²α = 2 L=P

Kokosimek: Dziękuje!