planimetria, kąty w kole
salamandra:
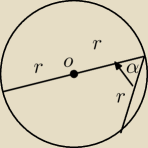
Kąt α przedstawiony na rysunku ma miarę równą:
60 stopni, ale jak to uzasadnić nie korzystając z własności 30,60,90?
24 lis 18:10
Adamm:
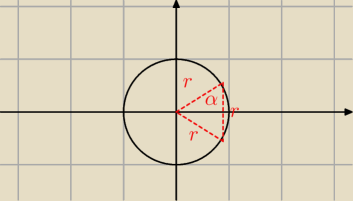
masz trójkąt równoboczny jak dorysujesz jeden z promieni
24 lis 18:15
a7:
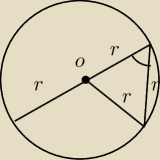
jest to trójkąt równoboczny o boku r, więc każdy kąt ma 60 stopni
24 lis 18:16
salamandra:
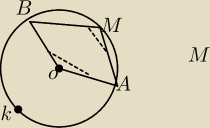
No racja, dzięki, a tutaj jak mam wywnioskować bez żadnej danej, ile ma kąt AOB?
Mam tylko powiedziane, że kąty (te z przerywaną linią) są równej miary
24 lis 18:20
Adamm:
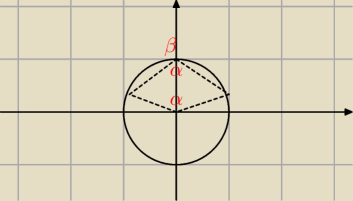
β = 2α = 360
o−α
24 lis 18:23
Adamm:
z kąta wpisanego i opisanego
24 lis 18:23
salamandra: Skąd wynika ta zależność? Gdzie jest kąt β, bo nie za bardzo z rysunku jestem w stanie
wywnioskować
24 lis 18:25
salamandra: Znaczy ok, ja wiem, że to jest 2α, tylko, że odpowiedź jest 120, do tego wyniku nie wiem jak
dojść bez żadnej danej
24 lis 18:27
Adamm:
kąt β to ten dopełniony do kąta AMB
24 lis 18:28
salamandra: Wiem, jednak skąd wynik 120 stopni?
24 lis 18:38
Adamm:
bo masz
2α = 360o−α
3α = 360o
α = 120o
24 lis 18:39
24 lis 18:58
 Kąt α przedstawiony na rysunku ma miarę równą:
60 stopni, ale jak to uzasadnić nie korzystając z własności 30,60,90?
Kąt α przedstawiony na rysunku ma miarę równą:
60 stopni, ale jak to uzasadnić nie korzystając z własności 30,60,90?
 masz trójkąt równoboczny jak dorysujesz jeden z promieni
masz trójkąt równoboczny jak dorysujesz jeden z promieni
 jest to trójkąt równoboczny o boku r, więc każdy kąt ma 60 stopni
jest to trójkąt równoboczny o boku r, więc każdy kąt ma 60 stopni
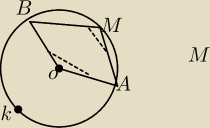 No racja, dzięki, a tutaj jak mam wywnioskować bez żadnej danej, ile ma kąt AOB?
Mam tylko powiedziane, że kąty (te z przerywaną linią) są równej miary
No racja, dzięki, a tutaj jak mam wywnioskować bez żadnej danej, ile ma kąt AOB?
Mam tylko powiedziane, że kąty (te z przerywaną linią) są równej miary
 β = 2α = 360o−α
β = 2α = 360o−α
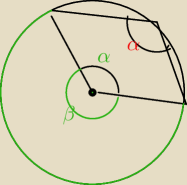 β=360−α β=2α (gdyż jest to kąt środkowy dwa razy większy od α−kąta wisanego (czerwonego)
opartego na tym samym łuku)
https://matematykaszkolna.pl/strona/465.html
360−α=2α ⇒ α=120
β=360−α β=2α (gdyż jest to kąt środkowy dwa razy większy od α−kąta wisanego (czerwonego)
opartego na tym samym łuku)
https://matematykaszkolna.pl/strona/465.html
360−α=2α ⇒ α=120