równanie trygonometryczne Ollie: Wiedząc, że 2sin²x+3sinx=0 znaleźć cosx Generalnie rozwiązałem to, ale nie wiem czy dobrze. Z równania wyszło mi x=kπ. Dalej skorzystałem z jedynki trygonometrycznej i wyszło mi, że x=1 v x=−1

Ollie: znaczy cosx=1 v cosx=−1

ICSP: sin(x)[2sin(x) + 3] = 0

	3
sin(x) = 0 v sin(x) = −
	2

sin(x) = 0 ⇒ cos(x) = ±1 Po co wyznaczałeś x = kπ ?

Ollie: Bo tak umiałem

Ollie: Dobra, ale tak poważnie, to nie wiem skąd z sinx=0 wynika, że cosx=±1

Ollie: Czy to właśnie z jedynki trygonometrycznej czy może z jakiejś innej własności o której nie wiem?

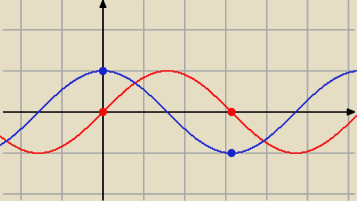
janek191: Popatrz na wykresy funkcji y = sin x i y = cos x

Ollie: No ok, wykresy wykresami, ale jak to zrobi analitycznie?

Mila: Ollie, czy ty chodziłeś na lekcje matematyki?

Mila: https://matematykaszkolna.pl/strona/397.html

salamandra: Skoro sinx= 0, to sin(0) = 0, więc to 0 jest jakby naszym "x", więc cosx = cos(0) = 1, dla przykładu

minxie: Chodziłem, ale niestety nie wszystko pojąłem, jak widać To może inaczej, bo sinx=0 to jest chyba za prosty przykład. Co gdybym miał np. sin x=0,35329847? Jak w tej sytuacji wyznaczyć cosx? Też każecie mi patrzeć na wykresy?

Mila: Jedynka trygonometryczna. sinx=0 sin²x+cos²x=1 cos²x=1 cosx=1 lub cosx=−1 jeśli nie masz ograniczeń na x. A wykresy powinieneś znać, przydają się i ułatwiają rozwiązywanie równań i nierówności tryg. Tabelę podaną w linku też zapamiętaj, najlepiej napisz sobie i zerkaj przy rozwiązywaniu zadań, to zapamiętasz.