średnia arytmetyczna i geometryczna bjkm: Wiedząc, że pierwiastek trzeciego stopnia ze średniej arytmetycznej długości boków trójkąta

	√6
jest odwrotnością średniej geometrycznej tych długości wykaż, że pole<
	4

bjkm: Pomoże ktoś z tym

Szkolniak: https://matematykaszkolna.pl/forum/372274.html

Godzio: Zaproponuję coś takiego, błędu nie widzę, a otrzymałem nieco mocniejszą nierówność

	1
3√(a+b+c)/3 =		, a stąd mamy abc(a + b + c) = 3
	3√abc

ab * ac + ab * bc + ac * bc = 3

	1		2P
P =		absin(α) ⇒ ab =		> 2P
	2		sin(α)

Jest możliwość, że jeden z kątów będzie miał miarę 90^o, wówczas nierówność byłaby nieostra: ab ≥ 2P, jednak pozostałe miary muszą być inne niż 90^o, a stąd otrzymamy nierówność ostrą, i dalej suma również pozostaje ostra. Analogicznie możemy zapisać nierówność dla pozostałych kombinacji boków: ac i bc 3 = ab * ac + ab * bc + ac * bc > 4P² + 4P² + 4P² = 12P²

1		1		√6
	> P2 ⇒ P <		<
4		2		4

Mila:

	√3
Ja otrzymałam dość łatwo nierówność P<		.
	4

Z √6 mi nie wychodzi.

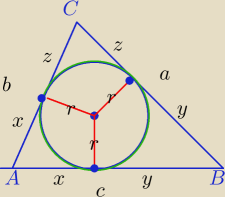
Mila: 1) W każdy Δ możesz wpisać okrąg. a,b, c − boki Δ a=z+y, b=z+x, c=x+y 2) obw=2x+2x+2z p=x+y+z− połowa obwodu P_Δ=√(x+y+z)*(x+y+z−x−y)*(x+y+z−z−y)*(x+y+z−z−x) P_Δ=√(x+y+z)*xyz 3) Z treści zadania :

	1
3√(2x+2y+2z)/3=		/3
	3√(x+y)*(y+z)*(x+z)

2*(x+y+z)*(x+y)*(y+z)*(x+z)=3 dalej próbuj sam

Mila: x>0,y>0, z>0