... basia: W trójkącie ABC mamy AB=40, BC=13, CA=37. Dwusieczna kąta ACB przecina bok AB w punkcie D. Wyznacz odległość punktu D od prostych AC i CB. Proszę o pomoc.

Bobo: Zacznij od: ∑√ABδ

basia: ...

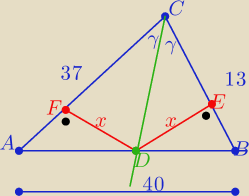
a@b: Punkt D leżący na dwusiecznej CD jest równo oddalony od ramion AC i BC kąta ACB to |DF|=|DE|=x

	x*37		x*13
P(ADC)=P1=		i P(DBC)=P2=
	2		2

P(ABC)=P₁+P₂= 25x Ze wzoru Herona

	37+13+40
P(ABC)= √p(p−37)(p−40)(p−13) , p=		= 45
	2

P(ABC=................ = 240 to 25x=240 ⇒ x=9,6

Basia : Czy to jest dobrze rozwiązane?

a@b: https://matematykaszkolna.pl/forum/393843.html

Mila: Bardzo dobrze jest rozwiązane. Są inne sposoby, ale więcej rachunków. 1) oblicz |AD| 2) Oblicz cos∡A 3) Rozwiązuj ΔAFD Powodzenia Basiu.

basia: dziękuję wszystkim za pomoc