asd asd: |x+1| + |x+2| = 1 −x−1−x−2 = 1 2x = −4 x=−2 i x<0 x+1+x+2 = 1 2x=−2 x= −1 o x>0 a rozwiazanie jest: <−2; −1>. Dlaczego nie wychodzi?

konrad: musisz rozpatrzeć 3 przypadki x∊(−∞,−2> , x∊(−2,−1> i x∊(−1,∞)

konrad: dla każdego przypadku rozwiązać równanie i na na koniec zsumować rozwiązania

asd: ale dlaczego wychodzi przedzial skoro tam jest znak rowna sie '=' https://matematykaszkolna.pl/strona/15.html wedlug tego wzoru podstawiam x i −x

nieznajomy : ponieważ twoje dziedziny poszczególnych przypadków są przedziałami, a w pewnym przypadku iksy mogą się zredukować i wtedy wychodzi załóżmy 1=1,co oznacza że każdy x z dziedziny spełnia to równanie

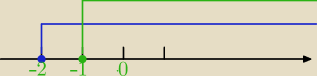
Mila: 1) |x+1|=x+1 dla x≥−1 |x+1|=−x−1 dla x<−1 2) |x+2|=x+2 dla x≥−2 |x+2\=−x−2 dla x<−2) a) x<−2 równanie ma postać: −x−1−x−2=1 −2x=4 x=−2∉(−∞,−2) b) x∊<−2,−1) −x−1+x+2=1 1=1 ⇔każda liczba x∊<−2,−1) spełnia równanie c) x≥−1 x+1+x+2=1 2x=−2 x=−1 ====== odp. x∊<−2,−1>

PW: Ponieważ |x+2| jest odkegłością między liczbami x i (−2), zaś |x+1| jest odległością między x i (−1), wystarczy narysować na osi liczby (−2) i (−1), aby zorientować się, że tylko dla x∊<−2, −1> suma odległości jest równa 1 (i oczywiście dla wszystkich x∊<−2, −1> suma odległości jest równa 1)..