Wartość bewzględna - funkcja
Patryk: Dla jakich wartości paramtru m równanie ma dokładnie dwa rozwiązania.
|x2−9| + |x2−16| = m
Wiem, że aby do rozwiązać, najlepiej naszkicować wykres, mógłby ktoś podpowiedzieć jak to
naszkicować? Gdy miałem pod wartością bezwzględną samego x to wiem, że rozwiązuje sie to
przedziałami, ale ten x2 jest troche inny przypadek i nie wiem już jak się za to zabrać
13 lis 19:54
Inka: |x2−9|
x2−9≥0 dla x∊(−∞ −3>U<3,∞)
x2−9<0 dla x∊*−3,3)
to samo zrob dla |x2−16|
x2−16= (x−4)(x+4)
x2−16≥0 dla x∊.......
x2−16<0 dla x∊...
i przedzialami
13 lis 19:59
ICSP: Funkcja f(x) = |x2 − 9| + |x2 − 16|
jest parzysta, więc szukasz tylko jednego rozwiązania dodatniego.
Dla x > 0 najpierw maleje, następnie w pewnym przedziale jest stała a na koniec zaczyna rosnąć.
Dlatego jedno rozwiązanie dodatnie będzie wtedy gdy przekroczy wartość w 0 tzn 25
m > 25
13 lis 20:05
Patryk: Ok, dostosuje się, dzięki za podpowiedź

13 lis 20:07
Patryk: Jeśli wyznacze przedziały dla wartości bezwzględnych kiedy ≥ i < 0 to później naszkicować
wykres z miejsc zerowych wgl. przedziałów?
13 lis 20:20
a@b:
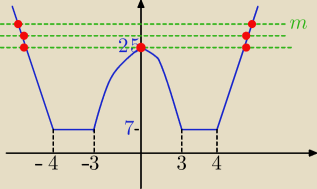
m>25
13 lis 20:27
13 lis 21:29

 m>25
m>25