funkcja kwadratowa
Nikto0: Witam.

Proszę o pomoc. dla jakich wartości parametru m pierwiastki równania
8(m+1)x
2−8mx+3m−2=0 spełniają warunek x
1+x
2=x
12+x
22
z warunku x
1+x
2=x
12+x
22 wychodzi mi m
1=2 i m
2=−1 z delty większej od zera m należy od
1 do 2. Jak to rozwiązać poprawnie?
13 lis 19:00
Inka:
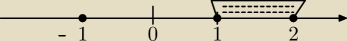
delta ≥0 bo nie masz dwa rozne pierwiastki
nie liczylem
wtedy z delty
m∊<.2>
z warunku m={−1,2}
wrzucasz na os liczbowa
reasumujac m∊<1,2>
13 lis 19:13
Tech: A to nie jest tak ze z warunku na pierwiastki wychodzi m=−2 i m=1/3 ?
13 lis 19:26
Tech: Przecież x=−1 wyrzucasz ze zbioru rozwiązań

?
13 lis 19:27
Inka: Nie wiem nie liczylem .Nie mam potrzeby tego liczyc
13 lis 19:28
Tech: Nawet jeśli, widać ze −1 nie należy do zbioru rozw gdyż mianownik ≠0 czyli odp m=−2 i m=1/3
13 lis 19:29
Inka: Przeciez wyrzucilem

13 lis 19:29
Tech: Zapisałeś w warunki na m={−1;2} a to już nie prawda
13 lis 19:31
Inka: Reasumujac m∊<1,2> tak napisalem
Warunek ten napisala kolezanka (ja nie liczylem bo mi sie nie chce liczyc
13 lis 19:33
Inka: Poza tym nie z warunku na m tylko z warunku (czyli warunku zadania ) m∊{−1,2}
13 lis 19:34
Tech: Tylko jako odpowiedz bierzesz cześć wspólna warunków 1) m∊[−2;1]. 2) m=−2 v m=1/3
Czyli m=−2 ⋀ m=1/3
13 lis 19:36
Inka: Byc moze jest tak jak piszesz .
Kolezanka nie przedstawila obliczen a mnie sie liczyc nie chce
13 lis 19:38
Inka: Zastanow sie nad postem 19 :36
A co z pozostalymi m .
13 lis 19:43
13 lis 21:49
a@b:
a= 8(m+1), b=−8m , c=3m−2
więc skąd u ciebie w mianowniku m2−1 ?
13 lis 21:55
a@b:
O jakim zadaniu Ty piszesz ?
Napisz jeszcze raz treść zadania
13 lis 22:01
Nikto0: Dla jakich wartości parametru m pierwiastki równania (m2−1)x2+(1−m2)x+m2−m−2 spełniają
warunek x1+x2=x12+x22 źle przepisałam zadanie
Teraz jest dobrze
13 lis 22:03
6latek: Wczoraj albo przedwczoarj rozwiazane mialas to
Nie porafisz dokonczyc prostego rownania ?
13 lis 22:06
Nikto0: Równanie potrafię dokończyć to tylko część rozwiązania tylko nie wiedziałam że może być tylko
jeden pierwiastek
13 lis 22:13
6latek: Jest tak
jesli masz napisane dwa rozne pierwiastki to wtedy Δ>0
Jesli masz napisane pierwiastki (bez rozne) to wtedy Δ≥0
bo na to zeby istnialy pierwiastki musi byc Δ>0 ale pierwiastek moze byc podwojny
np x
2−4x+4=0
Δ= 16−16=0
czyli masz pierwiastek podwojny
| | −b | | 4 | |
x12= |
| = |
| =2 x=2 pierwiastek (podwojny) |
| | 2a | | 2 | |
wiec mozesz zapisac sobie ze x
2−4x+4= (x−2)
2
13 lis 22:25
a@b:
Nie mąć w głowach!
Δ>0
13 lis 22:55
6latek: Tak robilem jak piszez to mnie poprawiano
13 lis 23:02
13 lis 23:03
14 lis 10:53
14 lis 12:12
ICSP: Tutaj nawet równania nie ma. To jest równanie :
(m
2 − 1)x
2 + (1 − m
2)x + m
2 − m − 2 = 0
Możemy założyć, że m ≠ ± 1 (mamy mieć dwa różne pierwiastki)
Dzieląc stronami przez m
2 − 1 dostajemy równanie:
| | m − 2 | | −3m +7 | | 7 | |
Δ = 1 − 4( |
| ) = |
| > 0 ⇒ (m−1)(3m − 7) < 0 ⇒ m ∊ (1 ; |
| ) |
| | m − 1 | | m − 1 | | 3 | |
Wzory Viete'a :
| | m − 2 | |
x1 + x2 = 1 i x1x2 = |
| |
| | m − 1 | |
(x
1 + x
2)
2 − (x
1 + x
2) − 2x
1x
2 = 0
x
1x
2 = 0
m = 2
14 lis 12:26
ICSP: Nie mam pojęcia co masz źle.
Nie widać tam żadnego porządku i o dziwo jest mniej opisów niż u mnie.
Żaden warunek nie jest zaznaczony.
Sprawdź moje wyniki ze swoimi i zobacz wychodzą różne.
14 lis 12:29
Nikto0: Liczyłam deltę (1−m2)2−4(m2−1)(m2−m−2) ze wzorów skróconego mnożenia rozbiłam (m2−1) i
(m2−m−2)
Potem porównałam do zera (1−m2)2
14 lis 12:38
Nikto0: później zaznaczyłam na wykresie miejsca zerowe wielomianu
14 lis 12:39
Nikto0: Teraz możesz wskazać co jest źle?

14 lis 12:45
ICSP: Δ = (m − 1)2(m+1)2 − 4(m−1)(m+1)(m−2)(m+1) = −4(m−1)3(m+1)4(m−2)
o to przekształcenie chce zapytać.
W jaki sposób z wielomianu stopnia IV zrobiłaś wielomian stopnia VIII ?
14 lis 12:53
ICSP: Najpierw przyrównujesz co do 0 − nie wiadomo po co

Potem liczysz deltę i wcale o tym nie informujesz ( brak znaku Δ )
Jeżeli ktoś będzie sprawdzał te notatki to się pogubi.
14 lis 12:55
Nikto0: bo (m−1) jest do kwadratu ale oprócz tego mam jeszcze jedno (m−1)
(m+1) jest do kwadratu ale jest jeszcze 2 razy (m+1)
14 lis 12:57
ICSP: No to wyciągasz przed nawias wspólny czynnik :
(m−1)(m+1)2
14 lis 12:58
Nikto0: Nie wiem jak to wyciągnąć przed nawias.
14 lis 13:03
Nikto0: A z tego wyjdzie dobry wynik?
14 lis 13:06
ICSP: Wiesz co masz wyciągnąć, więc możesz to zrobić brutalnie:
(m − 1)
2(m+1)
2 − 4(m−1)(m+1)(m−2)(m+1) =
| | (m−1)2(m+1)2 | | 4(m−1)(m+1)2(m−2) | |
= (m − 1)(m + 1)2[ |
| − |
| ] |
| | (m−1)(m+1)2 | | (m−1)(m+1)2 | |
Większość się skróci.
14 lis 13:08
Nikto0: Już rozumiem. a co potem?
14 lis 13:16
ICSP: Robisz dokładnie tak jak u Ciebie tylko z dobrze policzoną deltą :
Δ = (m − 1)(m + 1)2(−3m + 7)
14 lis 13:17
Nikto0: skąd wziołeś (−3m+7)?
14 lis 13:22
Jerzy:
Ty jesteś przytomna ? To jest wynik z nawiasu kwadratowego: ( m − 1) − 4(m − 2) = −3m + 7
14 lis 13:25
Nikto0: Dziękuję
14 lis 13:28
 Proszę o pomoc. dla jakich wartości parametru m pierwiastki równania
8(m+1)x2−8mx+3m−2=0 spełniają warunek x1+x2=x12+x22
z warunku x1+x2=x12+x22 wychodzi mi m1=2 i m2=−1 z delty większej od zera m należy od
1 do 2. Jak to rozwiązać poprawnie?
Proszę o pomoc. dla jakich wartości parametru m pierwiastki równania
8(m+1)x2−8mx+3m−2=0 spełniają warunek x1+x2=x12+x22
z warunku x1+x2=x12+x22 wychodzi mi m1=2 i m2=−1 z delty większej od zera m należy od
1 do 2. Jak to rozwiązać poprawnie?
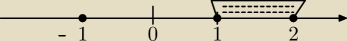 delta ≥0 bo nie masz dwa rozne pierwiastki
nie liczylem
wtedy z delty
m∊<.2>
z warunku m={−1,2}
wrzucasz na os liczbowa
reasumujac m∊<1,2>
delta ≥0 bo nie masz dwa rozne pierwiastki
nie liczylem
wtedy z delty
m∊<.2>
z warunku m={−1,2}
wrzucasz na os liczbowa
reasumujac m∊<1,2>
 ?
?




 Potem liczysz deltę i wcale o tym nie informujesz ( brak znaku Δ )
Jeżeli ktoś będzie sprawdzał te notatki to się pogubi.
Potem liczysz deltę i wcale o tym nie informujesz ( brak znaku Δ )
Jeżeli ktoś będzie sprawdzał te notatki to się pogubi.