trygonometria salamandra: Czy można nierówność trygonometryczną, a w sumie jakąkolwiek rozwiązać nie robiąc rysunku? Dla przykładu: cosx <= −U{√2{2}, gdy x ∊ <0; 2π > x=3/4π+2kπ v x= −3/4π+2kπ W przedziale <0;2π> x= 3/4π v x = 5/4π Czy bez rysowania rysunku tylko jakimiś koniunkcjami można dojść do wyniku x∊<3/4π; 5/4π>?

Mila: Trzeba narysować wykres, który jest przecież prosty.

salamandra: sinx+cosx>=1

	π
sinx+ sin(		−x) >= 1
	2

	x + π2−x		x − (π2−x)
2sin		cos		>=1
	2		2

	π		π
2sin(		)cos(x−		>=1
	4		4

	√2		π
2*		cos(x−		) >=1
	2		4

	π
√2cos(x−		) = 1 / *√2
	4

	π
2cos(x−		)= √2 / :2
	4

	π		√2
cos(x−		) =
	4		2

	π
x =		+ 2kπ v x= 2kπ
	2

	π		π
x∊<2kπ;		+2kπ>, a w odpowiedzi jest x∊<2kπ;		+kπ>
	2		2

Czy popełniłem gdzieś błąd rachunkowy?

Mila:

	π		√2
cos(x−		)≥		,
	4		2

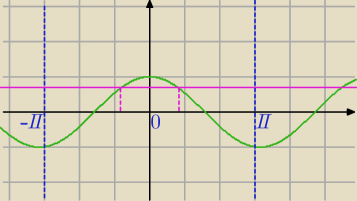
	π		π		π		π
x−		=		+2kπ lub x−		=−		+2kπ
	4		4		4		4

	π		π		π		π
−		+2kπ≤x−		≤		+2kπ /+
	4		4		4		4

	π
2kπ≤x≤		+2kπ
	2

salamandra:

	π
Czyli dobrze zrobiłem, nie wiem skąd w książce odpowiedź		+ kπ
	2

Mila:

salamandra: Jeszcze proste pytanie odnośnie nierówności, ponieważ wyznaczałem tylko w podanym przedziale i zazwyczaj wiekszą, a nie mniejszą, a los chciał, że wszedłem na tę stronę i kompletnie straciłem wątek: https://matematykaszkolna.pl/strona/1608.html:

	1
cosx <=
	2

	1
cosx =
	2

	π		−π
x=		+2kπ v x=		+2kπ
	3		3

	π		5
x∊<		+2kπ;		π+2kπ>
	3		3

Czy jest to wystarczająca odpowiedź?

Mila: Adres podałaś niepełny i nie otwiera się.

Mila:

	1
cos(x)≤
	2

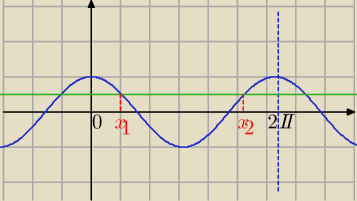
Teraz inny przedział wybieramy.

	π		π
x1=		+2kπ lub x2=2π−		+2kπ
	3		3

π		5π
	+2kπ≤x≤		+2kπ
3		3

ite: Podane za dużo, powinno być https://matematykaszkolna.pl/forum/392932.html

ite: Nie to oczywiście : ))) https://matematykaszkolna.pl/strona/1608.html

salamandra: Tak, przez dwukropek się nie otwierało, dziękuję za pomoc.