6latek: Punkt M ma wspolrzedne (m,0)
Punkt P ma wspolrzedne (0,p)
Zeby trojkat AMP byl trojkatem rownobocznym to musi zachodzic AM
2=AP
2=MP
2
{AM
2= (m−a)
2+a
2
{AP
2= (p−a)
2+a
2
MP
2= m
2+p^
Porownuje boki AM i AP
(m−a)
2+a
2= (p−a)+a
2
(m−a)
2=(p−a)
2
Teraz skorzystam z tozsamosci
x
2=y
2 ⇔x=y lub x=−y
m−−a=p−a
m=p
m−a=a−p
2a=m+p
m+p=2a
Porownuje bok AP z bokoiem MP
a
2+(p−a)
2= m
2+p
2
Zalozenie m=p
a
2+(p−a)
2= p
2+p
2
a
2+p
2−2pa+a
2−2p
2=0
2a
2−p
2−2pa=0
−p
2−2ap+2a
2=0 (tak uporzadkowalem z ewzgledu na p
p
2+2ap−2a
2=0
Δ=12a
2 √12a2= 2
√3a
| | −2a−2√3a | |
p1= |
| = −a−√3a= a(−1−√3) |
| | 2 | |
| | −2a+2√3a) | |
p2= |
| = −a+√3a=a(−1+√3) |
| | 2 | |
Tera warunek
m+p=2a m=2a−p)
a
2+(p−a)
2=(2a−p)
2+p
2
a
2+p
2−2pa+a
2= 4a
2−4ap+2p
2
−2a
2+2ap−p
2=0
−p
2+2ap−2a
2=0
p
2−2ap+2a
2=0
Δ= 4a
2−8a
2= −4a
2 Ten nie spelnia
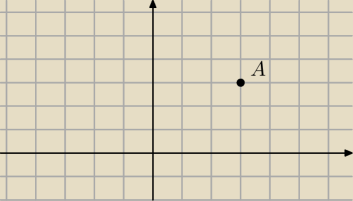 W ukladzie wspolrzednych prostokatnych dany jest ounkt A=(a,a) i a>0
Znajdz na osi OX taki punkt M i na osi OY taki punkt P zeby trojkat AMP byl trokatem
rownobocznym
W ukladzie wspolrzednych prostokatnych dany jest ounkt A=(a,a) i a>0
Znajdz na osi OX taki punkt M i na osi OY taki punkt P zeby trojkat AMP byl trokatem
rownobocznym

 Nawet wiesz zapomnialem .Wtedy nie pisalem zadan do zeszytu a teraz wlasnie to robie .
dziekuje
Nawet wiesz zapomnialem .Wtedy nie pisalem zadan do zeszytu a teraz wlasnie to robie .
dziekuje 