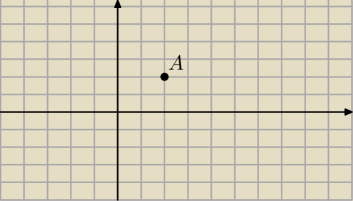
Trojkat rownoboczny 5-latek: W ukladzie wspolrzednych prostokatnych dany jest punkt A(a,a) a>0 Znajdz na osi OX taki punkt M i na osi OY taki punkt P aby trojkat APM byl rownoboczny

5-latek: Jedyne co teraz mi przychodzi na mysl to punkt M ma wspolraadna M(m.0) a punkt P(0,p) oraz ze MP= MA=PA

'Leszek: Dobrze zaczynasz , porownaj te dlugosci MA = PA. i otrzymasz n = m , nastepnie otrzymasz dla MP= MA rownanie kwadratowe i obliczysz : m = a(√3 − 1)

Adamm: 'Leszek, z MA=PA wcale nie wynika n=m

'Leszek: Wynika m = p , mam inne oznaczenia i dlatego inaczej napisalem , wysokosc trojkata AMP ma rownanie y = x .

Adamm: nie, nie wynika

'Leszek: A to dlaczego ?

Adamm: ponieważ z x²=y² nie wynika wcale x=y

'Leszek: Dla pierwszej cwiertki wynika , to byly wskazowki rozwiazania , a nie pelne rozwiazanie , wiec nie dziel wlosa na czworo , Ty tez podajesz nie pelne tylko czesciowe rozwiazania nie badz " bardziej swiety niz Papierz ! "

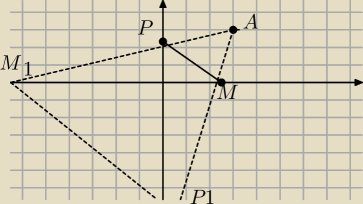
5-latek: Mysle ze bedzie taka sytuacja wedlug mnie tak {AM²= (a−m)²+a² {MP²= m²+p² {AP²= a²+(a−p)² Wiec trojkat AMP bedzie rownoboczny gdy AM²=MP²=AP² {AM²= a²−2am+m²+a²= 2a²−2am+m² {MP²= m²+p² {AP²= a²+a²−2ap+p²= 2a²−2ap+p² czyli {AM²= 2a²−2am+m² {MP²= m²+p² {AP²= 2a²−2ap+p² Teraz co mam z robic dalej ?

Adamm: czasami lepiej jest nie rozwijać pewnych potęg, później trudno jest cokolwiek zauważyć taka sytuacja jest tutaj porównując AM² z AP² dostaniesz a²+(a−m)²=a²+(a−p)² skąd m+p=2a lub m=p nie wiadomo czy w zadaniu proszą o konkretne punkty, czy o wszystkie takie punkty, więc lepiej podać wszystkie dalej rozpatrujesz kiedy m=p, a kiedy m+p=2a, dla każdego z przypadków porównujesz z kwadratem trzeciego boku, i rozwiązujesz równanie kwadratowe, by obliczyć jedną ze zmiennych

5-latek: Teraz mam porownac AM² z MP² i AP²z MP² ? To dostane {2a²−2am+m²= m²+p² {2a²−2ap+p²= m²+p² {2a²−2am=p² {2a²−2ap=m²

5-latek: jednak mam kloppot dalej

Adamm: a²+(a−m)²=a²+(a−p)² (a−m)²=(a−p)² a−m=a−p lub m−a=a−p m=p lub m+p=2a załóżmy że m=p wtedy a²+(a−p)²=m²+p² skoro m=p a²+(a−m)²=2m² 0=m²+2am−2a² 3a²=(m+a)² m+a=√3a lub m+a=−√3a m=(√3−1)a lub m=(−√3−1)a mamy zatem 2 rozwiązania m=p=(√3−1)a oraz m=p=(−√3−1)a (m oraz p mogą być ujemne) teraz załóżmy że m+p=2a wtedy p=2a−m a²+(a−p)²=m²+p² a²+(m−a)²=m²+(m−2a)² 0=m²−2am+2a² −a²=(m−a)² to być nie może zatem jedyne rozwiązania to m=p=(√3−1)a oraz m=p=(−√3−1)a

5-latek: Pozniej wroce do tego

5-latek: dziekuje Ci .

Metis:

5-latek: Witaj i napisz co u Ciebie . Teraz czytalem o manifestacjach .Zgroza Michal .