Przekształcanie wykresów funkcji trygonometryc salamandra: Mam pytanie odnośnie przekształcania wykresów funkcji trygonometrycznych. Dokładnie funkcji cos 1/2x: https://matematykaszkolna.pl/strona/1536.html Na filmiku matemaksa jest pokazane podstawienie np. f(x) = sin4x czyli f(π/2) = sin(2π) = 0 Idąc tym tokiem, dla cos 1/2x: f(π) = cos(π/2) = − 1, a jest wrecz przeciwnie, to dla 2π funkcja cos1/2x ma wartość −1

6latek: Masz funkcje postaci y=f(k*x) Stosujesz powinowactwo prostokatne o osi OY i skali k dla k>1 oznacza to sciskanie wykresu k razy wzdluz osi OX

	1
dla 0<k<1 oznacza to rozciaganie wykresu		razy wzdluz osi OX
	k

6latek: Oznacza to ze y=cosx rozciasz 2 razy wzdluz osi OX i masz wykres

Saizou : A ile to:

	π
cos		= ?
	2

Mila:

	1
f(x)=cos(		x)
	2

	1
cos(		x)=0⇔
	2

1		π
	x=		+kπ⇔
2		2

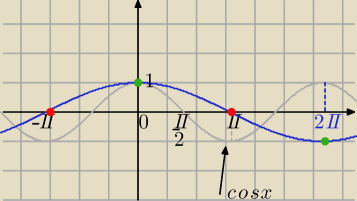
x=π+2kπ k=0,±1,±2,... x∊{π,−π,3π,−3π,5π,−5π....}

	1
cos		x=1
	2

1
	x=0+2kπ
2

x=4kπ x∊{0,4π,−4π,...}

	1
cos(		x=−1
	2

1
	x=π+2kπ
2

x=2π+4kπ x∊{2π,−2π,6π,−6π,.... Wykres jest "rozciągnięty". T=4π

salamandra: Mila no ok, ale w pierwszym równaniu wychodzi 2kπ, więc nie wychodzi T = 4π

Mila: Rozwiązanie tego równania to co innego niż wyznaczenie okresu tej funkcji.

	1
f(x)=cos(		x)
	2

okres zasadniczy funkcji g(x)=cosx to T=2π

	2π
okres f(x)=		=4π
	1   2

Możesz z definicji wyznaczyć. f(x+s)=f(x), s>0 i s nie zależy od x

	x+s)		1
cos(		)=cos		x
	2		2

x+s		1		x+s		1
	=		x+2kπ lub		=−		x+2kπ
2		2		2		2

x+s=x+4kπ⇔s=T=4kπ z drugiego wyjdzie sprzeczność

Mila: źle zapisałam okres f(x):

	2π
T=
	1   2

T=4π