proszę o pomoc bjkm: Oblicz długość trzeciego boku trójkąta wpisanego w okrąg o średnicy D i dwóch bokach trójkąta

	3		√3
		D i		D
	4		2

bjkm: mógłby ktoś szybko pomóc

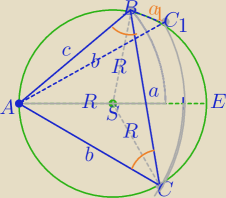Mila: |AE|=d=2R

	3
|AB|=c=		d
	4

	√3
|AC|=b=		d
	2

1)W ΔABC:

a
	=2R=d⇔a=d*sin(A)
sinA

Z tw. cosinusów: a²=c²+b²−2bc*cosA

	3		√3		3		√3
(d2 sin2A)=(		d)2+(		d)2−2*		d*		d*cosA /: d2
	4		2		4		2

	9		3		3√3
sin2A=		+		−		cosA
	16		4		4

	21		3√3
1−cos2A=		−		cosA
	16		4

	3√3		5
cos2A−		cosA+		=0
	4		16

	27		20		7
Δ=		−		=
	16		16		16

	3√3   √7   − 4   4		3√3−√7
cosA=		=		≈0.32
	2		8

lub

	3√3+√7
cosA=		≈0.98
	8

	21		3√3		3√3−√7
a2=		d2−		d2*
	16		4		8

lub

	21		3√3		3√3+√7
a2=		d2−		d2*
	16		4		8

dokończysz sam?

Eta: Inny sposób

	√3		3
b=		d , c=		d
	2		4

z tw. sinusów

b		√3
	=2R=d ⇒ sinβ= b/d⇒ sinβ=		⇒β=60o lub β=120o
sinβ		2

to cosβ= 1/2 lub cosβ= −1/2 z tw. cosinusów b²=a²+c²−2ac*cosβ dla cosβ=1/2 a²=b²−c²+ac ⇒ a=........... dla cosβ= −1/2 a²=b²−c²−ac ⇒ a=...

Mila: Dobry wieczór Eto, zobacz tam, masz taki sam wynik? https://matematykaszkolna.pl/forum/392079.html

Eta: Witam Jest ok

Mila: Dziękuję.

Mila: