planimetria guest: Wykaż, że w dowolnym trójkącie ABC zachodzi następująca zależność między długością boków

	a2−b2		sin(α−β)
a, b, c, a miarami kątów α, β, γ, :		=
	c2		sinγ

z góry dzięki za pomoc

guest: okej już znalazłęm na forum link dla zainteresowanych https://matematykaszkolna.pl/forum/324599.html

jc: a = 2R sin α, itd. R= promień okręgu opisanego. (a²−b²)/c² = (sin²α − sin²β)/sin²γ sin γ= sin(α+β) Równość z zadania jest równoważna równości sin²α − sin²β = sin(α+β)sin(α−β) Prawa strona = sin²α cos²β − sin²β cos²α = sin²α − sin²β = Lewa strona

Eta:

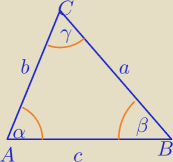
Mila: α+β+γ=π Z tw. sinusów:

a
	=2R⇔a=2R sinα
sinα

Analogicznie : b=2Rsinβ, c=2R sinγ

	a2−b2		4R2sin2α−4R2 sin2β		sin2α−sin2β
L=		=		=		=
	c2		4R2 sin2γ		sin2γ

=

	(sinα−sinβ)*(sinα+sinβ)
=		=
	sin2γ

	α+β   α−β   α+β   α−β   2cos *sin *2*sin *cos   2   2   2   2
=		=
	sin2γ

	sin(α+β)*sin(α−β)		sin(α−β)
=		=		=P
	sin2γ		sinγ

[sinγ=sin(π−(α+β))=sin(α+β)] ====================

jc: sin(α+β)=sin α cos β + sin β cos α sin(α−β)=sin α cos β − sin β cos α sin(α+β) sin(α−β) = sin²α cos²β − sin²β cos² =sin²α (1− sin²β) − sin²β (1−sin²α) =sin²α − sin²β

Eta: A czym to się różni od poprzednich ?

jc: Wzory na funkcje sumy wydają się bardziej podstawowe niż wzory na różnice funkcji. Pamiętam tylko te pierwsze.

Eta: Moje pytanie było skierowane do Mili Często się zastanawiam,że jej się tak chce bez potrzeby dublować rozwiązania

Eta: https://matematykaszkolna.pl/forum/324599.html

Mila: Zaczęłam pisać, gdy nie było żadnego wpisu, tak trudno to zrozumieć?

jc: Tak, jak ja. Pisząc nie widzimy nowych wpisów.