Nierówność wymierna z wartością bezwzględną w liczniku. Bart: Wiem, że to zadanie już się tutaj pojawiło ale podpowiedzi forumowiczów nie naprowadziły mnie do poprawnego rozwiązania Link do wcześniejszego posta: matematyka.pisz.pl/forum/312637.html | x − 2 |/x < x Podejrzewam, że ciągle przyjmuję złe założenia, mimo że mnożę przez x². Czy mógłby ktoś to zrobić krok po kroku? Byłbym ogromnie wdzięczny

kerajs: 1) Dla x<0 masz

−x+2
	<x
x

−x+2>x² (x+2)(x−1)<0 −2<x<0 2) Dla 0< x<2 masz

−x+2
	<x
x

−x+2<x² (x+2)(x−1)>0 1<x<2 3) Dla x≥2 masz

x−2
	<x
x

x−2<x² x≥2 ostatecznie: −2<x<0 v x>1

Mila: 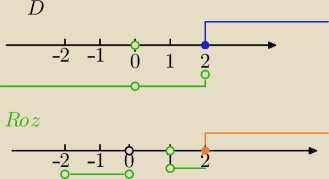312637

| x−2 |
	<x
x

x≠0 1) |x−2|=x−2 dla x≥2 wtedy mianownik dodatni

x−2
	<x /*x
x

x−2<x² x²−x+2>0 i x≥2 Δ=1−8<0 ⇔trójmian przyjmuje wartości dodatnie dla każdego x∊<2,∞) lub 2) |x−2|=−x+2 dla x<2 wtedy mamy nierówność:

−x+2
	<x
x

dla x∊(0,2) mnożymy obustronnie przez x bez zmiany kierunku nierówności −x+2<x² x²+x−2>0 Δ=9 x=−2 lub x=1 x<−2 lub x>1 i x∊(0,2)⇔x∊(1,2) lub dla x<0 U{−x+2}{x|<x /*x teraz zmienimy kierunek nierówności −x+2>x² x²+x−2<0 x∊(−2,1) i x<0⇔ x∊(−2,0) Z (1) i (2) x∊(−2,0)∪(1,∞) ================== Jeżeli obie strony tej nierówności pomnożysz przez x² to masz równanie 3 stopnia z wartością bezwzględną.

Bart: Dziękuje za poświęcenie mi czasu, już rozumiem

Mila: