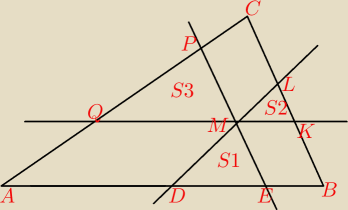
 Wewnątrz trójkąta ABC leży punkt M. Przez punkt M poprowadzono trzy proste:
• równoległą do AB, która przecięła boki BC oraz AC w punktach odpowiednio K oraz Q,
• równoległą do BC, która przecięła boki AC oraz AB w punktach odpowiednio P oraz E,
• równoległą do AC, która przecięła boki AB oraz BC w punktach odpowiednio D oraz L
Wykaż, że jeżeli [MDE] = S1, [MKL] = S2 i [MPQ] = S3, to pole trójkąta ABC jest równe
(√S1 + √S2 + √S3)2
.
Wewnątrz trójkąta ABC leży punkt M. Przez punkt M poprowadzono trzy proste:
• równoległą do AB, która przecięła boki BC oraz AC w punktach odpowiednio K oraz Q,
• równoległą do BC, która przecięła boki AC oraz AB w punktach odpowiednio P oraz E,
• równoległą do AC, która przecięła boki AB oraz BC w punktach odpowiednio D oraz L
Wykaż, że jeżeli [MDE] = S1, [MKL] = S2 i [MPQ] = S3, to pole trójkąta ABC jest równe
(√S1 + √S2 + √S3)2
.
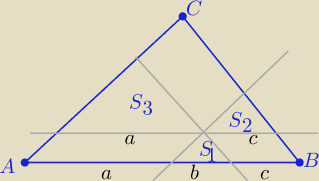 Wszystkie trójkąty o polach S1,S2,S3 są podobne do trójkąta ABC o polu S
to stosunek pól jest równy kwadratowi skali podobieństwa
zatem
Wszystkie trójkąty o polach S1,S2,S3 są podobne do trójkąta ABC o polu S
to stosunek pól jest równy kwadratowi skali podobieństwa
zatem
| a | S3 | a | √S3 | |||||
( | )2= | ⇒ | = | |||||
| a+b+c | S | a+b+c | √S |
| b | √S1 | |||
i | = | |||
| a+b+c | √S |
| c | √S2 | |||
= | ||||
| a+b+c | √S |
| a+b+c | √S1+√S2+√S3 | ||
= | |||
| a+b+c | √S |



 Taki jest zwyczaj na forum.
Taki jest zwyczaj na forum.
