. anonim: W równoległoboku ABCD kąt przy wierzchołku A ma miarę 45° oraz |AB| = 16, |BC| = 12. Na boku AB leży taki punkt K, że |AK| = 12, a na boku BC leży taki punkt L, że |BL| = 3. Odcinki DL i CK przecinają się w punkcie M. Oblicz pole czworokąta BLMK.

Mila:

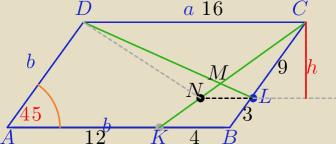
	1
1) [KBC]=		*4*12*sin45o=12√2
	2

	|NL|		4
2) ΔNLC∼ΔKBC⇔		=		⇔
	9		12

|NL|=3 3) Z trapezu oblicz pole ΔMLC 4) [BLMK]=12√2−[MLC]

Mila: albo 3) możesz obliczyć P_NLM korzystając z podobieństwa ΔNLM i DCM.

anonim: jak mam wyznaczyć pole PNLM? nie mogę tego obliczyć

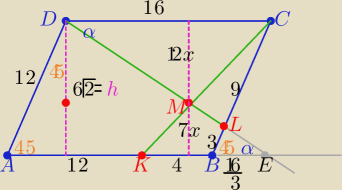
Eta: P(BLMK)=S , S=P(KEM)−P(BLE) i h=6√2 z podobieństwa trójkątów BLE i DCL w skali k= 1/3 to |BE|=16/3

	1		16		√2
P(BLE)=		*3*		*		⇒ P(BLE)=4√2
	2		3		2

z podobieństwa trójkątów KME i DMC i |KE|=28/3 to KE/DC=7/12 to h=19x ⇒ x=6√2/19 to 7x=42√2/19

	1		28		42√2
P(KEM) =		*		*		=..............
	2		3		19

S=......................... S= 120√2/19 ==============

Mila: Jeżeli Anonim chce dokończyć sposób z 20:48 to proszę pisać

anonim: chcę wiedzieć po prostu jak wyznaczyć właśnie taką część pola trapezu, z jakiej własności to wynika, o ile tak się da

Mila: Piszę.

Mila:

	9√2
1) W ΔCEL: h=
	2

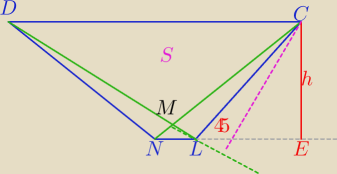
	1		9√2
PΔDCL=		*16*		=36√2
	2		2

Narysuję tylko trapez DCLN.

	3
ΔNLM∼ΔDCM w skali k=		⇔
	16

|DM|		3
	=
|ML		16

ΔDMC i ΔCML mają wspólną wysokość opuszczoną na DL z wierzchołka C⇔

PΔDMC		3
	=		⇔
PΔCML		16

	3
PΔDMN=s , PΔCML=		s
	16

	3
s+		s=36√2
	16

19
	s=36√2
16

	36√2*16
s=
	19

	3		3		36√2*16		108√2
PΔCML=		s=		*		=
	16		16		19		19

2) Wracamy do poprzedniego zapisu:

	108√2		228−108)
[BLMK]=12√2−[MLC]=12√2−		=√2*(
	19		19

	120√2
[BLMK]=
	19

==================== II Sposób 1) Obliczyć wysokość ΔNLM 2) Obliczyć pole ΔNLM 3) Obliczyć pole trapezu KBLN i zsumować. Spróbuj. ( o ile chcesz się tego nauczyć)

anonim: dzięki bardzo

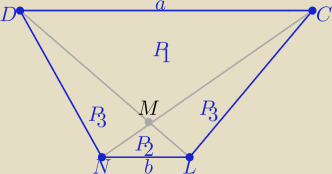
Eta: P−− pole trapezu , k −− skala podobieństwa ΔNLM i DCM P1=k²*P₂ , P₃=k*P₂ P=P₁+2P₃+P₂ = k²P₂+2kP₂+P₂= (k²+2k+1)P₂⇒ P=(k+1)²*P₂ to

	P		k2*P		k*P
P2=		, P1=		, P3=
	(k+1)2		(k+1)2		(k+1)2

================================

	16+3		9√2		19*9√2
W tym zadaniu P=		*		=
	2		2		4

k=16/3

	16		19*9√2		3*3
P3=		*		*
	3		4		19*19

	108√2
P3=
	19

=============

Mila: Odwrotną proporcję dałam, mam nadzieję, że zauważyłeś Powinno być:

DM		16
	=
ML		3

[DMC]		16
	=
[CML]		3

	3
[DMC]=s to [CML]=		s
	16

dalej dobrze. Do wiadomości:

	3
[DMN]=[CML], [NLM]=(		)2*s
	16