prawdopodobienstwo calkowite Kuba: W dwóch pudełkach znajdują się losy. W pierwszym pudełku 40% losów jest pustych, a w drugim 70%. Gracz wybiera po jednym losie z każdego pudełka. Obliczyć prawdopodobieństwo, że: a) obydwa losy wygrywają Czy to jest dobrze i zawsze można w taki sposób zapisywać prawdopodobieństwo całkowite? Jeśli nie, to jak?

	6 1		6		3 1		3
P(A)=		*		+		*
	10 6		10		10 3		10

ite: Czy każde z pudełek może być wybrane z jednakowym prawdopodobieństwem?

ite: Źle przeczytałam treści zadania, sorry.

Kuba: Tak, nie ma zadnej informacji, zeby mialo byc inaczej

ite: 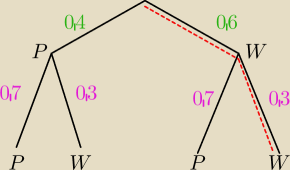wybór losu z pierwszego pudełka wybór losu z drugiego pudełka a) prawdopodobieństwo, że obydwa losy wygrywają 0,6*0,3

ite: P − wybór losu pustego W − wygrywającego

Kuba: Dzieki, tylko ja potrzebuje umieć rozwiązać takie zadanie ze wzoru na prawdopodobieństwo

	n k
całkowite i nie wiem czy zawsze zapisuje to z tym

ite: 1/ Wzór na prawdopodobieństwo całkowite byłby przydatny, gdyby oba losy wyciągano tylko z jednego z tych dwóch pudełek. Czyli najpierw wybór pudełka, potem tylko z niego oba losy. Spróbuj obliczyć prawdopodobieństwo, że oba losy wybrane w taki sposób wygrywają.

	n k
2/ Współczynnik dwumianowy		wykorzystujesz do obliczeń, gdy masz ilość (a nie

procentowy udział) losów wygrywających i przegrywających w pudełku. Tutaj nie ma po co go używać.

Kuba: Ale jeśli będę miał takie samo zadanie, ale będę losował 5 razy i dajmy na to 3 razy wygrywam i 2 razy przegrywam. Wtedy zrobienie tego drzewkiem będzie męczarnią, więc jak to inaczej zapisac?

ite: Z ilu pudełek będą wyciągane te losy?

Kuba: To samo zadanie, czyli 2 pudelka i np b) gracz wybiera 3 losy wygrywające i 2 przegrywające

ite: Tutaj to dopiero będzie liczenia : ) Ze zwracaniem czy bez? Jak losowano po jednym losie, to nie miało znaczenia, teraz jest ważne. Po ile losów z każdego pudełka, przedtem było pół na pół, teraz się tak nie da.

ite: Najlepiej skorzystać z gotowego zadania z jakiegoś zbioru.

Kuba: Właśnie o to mi chodzi, że liczenie tego drzewkiem to jest po prostu cała strona kartki i tylko czekanie, żeby sie pomylić, nie prosze o rozwiązywanie tego, bo to bez sensu i drzewkiem to ja umiem to policzyć, tylko nie da sie tego zrobić w żaden inny sposób, np właśnie przez wzór na prawdopodobieństwo całkowite?

ite: Prawdopodobieństwo całkowite ma zastosowanie, gdy są dwie, trzy lub więcej wykluczających się możliwości o określonym prawdopodobieństwie wyboru : albo losy wyjmiemy tylko z tego albo tylko z innego pudełka. W zadaniu z 11:58 nie wybierasz najpierw tylko jednego z pudełek, więc nie ma powodu stosować wzoru na p.całkowite. Drzewka użyłam, bo wydawało mi się, że łatwiej mi będzie tłumaczyć z jego pomocą. Mogłam od razu zastosować wzór na niezależność zdarzeń 1021: P_1W − prawdopodobieństwo wylosowania losu W z pierwszego pudełka P_2W − p. wylosowania losu W z drugiego pudełka P_1W∩2W − p. wylosowania losów W z obu P_1W∩2W=P_1W*P_2W=0,6*0,3 Nie umiem tego lepiej wytłumaczyć...

Kuba: Okej, teraz juz rozumiem, dzięki wielkie za pomoc