matematykaszkolna.pl
Oblicz długość promienia okręgu opisanego na trójkącie dab: Oblicz długość promienia okręgu opisanego na trójkącie, jeśli długości boków tego trójkąta są równe √3, 2, 3
15 maj 21:45
daras: wiesz gdzie znajduje się środek tego okręgu ?
15 maj 21:50
Jerzy: Sam jestem ciekawy gdzie ?
15 maj 21:53
dab: nie wiem
15 maj 21:58
jc:
 abc 
R=
 4P 
15 maj 22:04
jc: 4P=2√11
15 maj 22:07
daras: https://matematykaszkolna.pl/strona/541.html
15 maj 22:10
dab: jak obliczyć pole?
15 maj 22:29
Mila: Twierdzenie cosinusów znane?
15 maj 22:39
jc: Wzór Herona?
15 maj 22:44
dab: niestety nie
15 maj 22:45
Mila: Przy takich bokach Heron zbyt skomplikowany chyba . Lepiej kierować się na twierdzenie sinusów.
15 maj 22:46
Mila: W takim razie dab licz pole ze wzoru Herona. Ładnie się liczy.
15 maj 22:57
PW: Umieścić trójkąt w układzie współrzędnych, tak by wierzchołek A był w punkcie (0, 0), wierzchołek b=B w punkci (0, √3), a wierzchołek C w pierwszej ćwiartce. Założyć, że |AC| = 3 i |BC| = 2. Łatwo obliczymy współrzędne punktu C. Właściwie potrzebna nam jest druga współrzędna punktu C − jest ona równa
 √11 
,
 √3 
 1 √11 1 
a więc pole trójkąta P =
√3
=
√11, jak podał jc o 22:07.
 2 √3 2 
15 maj 23:00
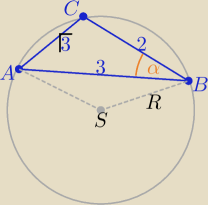
Eta: rysunek (bez obliczania pola) Trójkąt ABC jest rozwartokątny bo 22+(√3)2 <32 kąt ACB −− jest rozwarty Z tw. cosinusów
 4+9−3 5 
cosα=
=
to sinα= √1−2536 = √11/6
 2*2*3 6 
 √3 
z tw. sinusów
=2R
 sinα 
⇒ R=3√33/11 ============
16 maj 00:05
daras: no właśnie ładnie się liczy ale za kogoś emotka
17 maj 21:32
Eta: Dla daras ....... emotka emotka
17 maj 21:56
daras: wolę
20 maj 13:33
Eta: z
20 maj 17:38