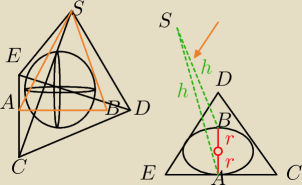
kula w czworoscianie foremnym salv: Kula wpisana w czworoscian foremny. Po prawej moja próba przedstawienia widoku z góry na ten czworościan,mam problem ze zwizualizowaniem sobie tego przekroju : https://matematykaszkolna.pl/forum/36896.html Wiem,że z góry nie byłoby widać tego trójkąta zielonego w przekroju,ale czy to wygląda tak jak nabazgralem?Bo te h od strony boku |EC| to ok,wiadomo,znajduje sie na scianie bocznej SEC ale na jakiej scianie bocznej znajduje się ta druga wysokość |SB|?Czy ona po prostu się nie znajduje na ścianie bocznej,ale również ma długość taka,jak |SA|?

6latek : https://zapodaj.net/8c428bd23bcb7.jpg.html https://zapodaj.net/4768ff2408d5d.jpg.html https://zapodaj.net/351792026b38f.jpg.html https://zapodaj.net/151d2cd7a2958.jpg.html Moze sie przyda . Z ksiazki Ciekawy czworoscian A. Ehrenfeucht (1966)

salv: Faktycznie ciekawy,sprawdze,dziękuje

ite: 1/ Punkt S jest wierzchołkiem, pkt B należy do podstawy czworościanu. Pozostałe punkty odcinka SB (nie wiem dlaczego nazywasz go wysokością) nie należą do żadnej ściany bocznej, lecz do wnętrza czworościanu. SB ma długość taką samą jak odcinek SA. Na rysunku Bogdana twoje S oznaczone jest jako C. 2/ r to nie są promienie, tylko długości odcinków, skąd wziął się okrąg o średnicy AB?

salv:

	a√3
Myślałem,że są to promienie okręgu wpisanego w trójkąt CED o dlugości		,a o |SB|
	6

myślałem jako o wysokości ściany bocznej jakiejś w środku (bo skoro jest styczna kula do wysokości ścian bocznych czworościanu,to szedłem w tym kierunku),nie wiedziałem,że można tak przekrój zrobić,bo nie wiem skąd wynika to,że |SB|=|SA|,z tego faktu właśnie styczności?

salv: Czyli widok z góry na ten czworościan,czyli okrag wpisany w trojkat rownoboczny bedzie mial jakies inne promienie?oczywiscie rozrozniam promien kuli wpisany w czworoscian od promienia okregu w podstawie

ite: Jeśli tak, to |AB|=2r się zgadza. r to rzeczywiście promień okręgu wpisanego w trójkąt CED (czyli podstawę czworościanu). Myślałam, że może chodzić o rzut wpisanej kuli na podstawę i dlatego zaprotestowałam.

salv: Dziękuje za pomoc (chociaż jeszcze nie pogardzę wyjaśnieniem od kogoś,dlaczego |SB|=|SA|..)

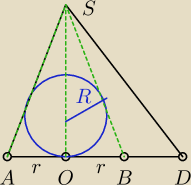
ite: Koło wielkie kuli jest wpisane wΔABS. |SB|=|SA| można uzasadnić właśnie tym, że pkt O i B zostały wyznaczone przez wpisanie w podstawę ABC okręgu. Wynika stąd, że |AO|=|BO|, SO jest wysokością czworościanu jest więc prostopadłe do płaszczyzny podstawy, więc SO⊥AB. ΔSAO i ΔSBO są przystające (bkb)→ |SB|=|SA|

salv: dziekuje

iteRacj@: Jeszcze dodaję model takiej kuli wpisanej w czworościan: https://www.geogebra.org/3d/wtmrcfmw