bryły obrotowe Kaś;*: Oblicz objętośc kuli wpisanej w czworościan foremny o krawędzi długości a

Bogdan:

	1		1		1		2
h =		a√3, r =		a√3, p =		(2r + 2h) = r + h =		a√3
	2		6		2		3

	1
H = √h2 − r2 =		a√6
	3

	1		1
Pole trójkąta ABC: PΔ =		* 2r * H =		a2√6 i PΔ = p*R
	2		6

	PΔ		1   a2√6   6
R =		=		= ...
	p		2   a√3   3

	4
Objętość kuli V =		πR3 = ...
	3

etka: mozna lepszy rysunek poprosić

Eta: Lepszego.... to ja nie widziałam

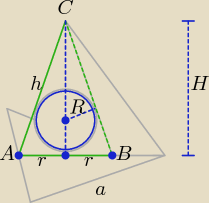
etka: etusiu tylko problem jest w tym ze ja nie wiem co to jest za trojkat ten na zielono

etka: i wogole te rachunki BOHDANA sa dla mnie nie zrozumiałe

Eta: kula jest styczna do wysokości w ścianach bocznych czyli zielony trójkąt a w niego wpisany okrąg ( jest to przekrój)

etka: oh etusiu jak ty pięknie to tłumaczysz dziękuje