Wyznacz zbiór wartości Yf (pochodna) salamandra: Wyznacz zbiór wartości Yf funkcji f okreslonej wzorem: f(x)= x²−1 −−−− x²+1 Wychodzi mi pochodna f'(x) = 0, i nie wiem jaki krok dalej podjąć

salamandra: nieaktualne, źle obliczyłem pochodną, pochodna wyjdzie jednak 4x

Satan: Kiedy poznać, że pochodna źle obliczona? Tylko pierwsza pochodna z funkcji stałej jest równa 0

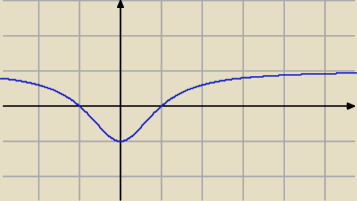
PW: Rysunek jest podsumowaniem rozważań poniżej.

	x2+1−2		2
f(x) =		= 1 −
	x2+1		x2+1

	2
Ułamek		przybiera wartość największą, gdy x=0, tak więc najmniejszą wartością
	x2+1

funkcji f jest

	2
1 −		= −1.
	1

	2
Ułamek		nie osiąga wartości najmniejszej, dla x→∞ dąży do 0 osiągając wartości
	x2+1

dodatnie, zatem f osiąga wartości mniejsze od 1 i f(x)→1 dla x→∞ lub dla x→−∞. Odpowiedź: Zbiorem wartości funkcji f jest <−1, 1), co wynika z ciągłości f.

Mila: II sposób w− wartość f(x)

x2−1
	=w
x2+1

x²−1=wx²+w x²−wx²=w+1 x²*(1−w)=w+1 w≠1

	w+1
x2=
	1−w

	w+1
równanie ma rozwiazanie dla		≥0 i w≠1
	1−w

(w+1)*(1−w)≥0⇔ w∊<−1,1) Zw_f=<−1,1)

Mila: Dobry wieczór PW, możesz tam spojrzeć? https://matematykaszkolna.pl/forum/389545.html

PW: No i wcale pochodna nie była potrzebna