Dany jest sześcian ABCDEFGH , którego krawędź ma długość 15 . Punkty Q i R dziel maturzystka: Dany jest sześcian ABCDEFGH , którego krawędź ma długość 15 . Punkty Q i R dzielą krawędzie HG i FG w stosunku 2 : 1 , to znaczy HQ = FR = 10 . Płaszczyzna AQR przecina krawędzie DH i BF odpowiednio w punktach P i S. Oblicz długości odcinków DP i BS . Proszę bez przedłużania EF i QR, bo szukam innego rozwiązania...

Maciess: Też mi to rozwiązanie nie pasowało, bo ja na egzaminie raczej bym tego nie zauważył. Zaraz spróbuje coś wykombinować

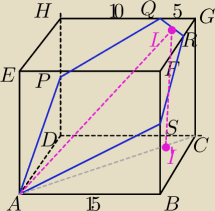
Maciess: Spróbuje z tego różowego trojkąta obliczyć kąt nachylenia przekroju do podstawy i potem coś dalej kombinować

Maciess: No i od razu zakładam, że |DP|=|BS|

maturzystka: Wiem, że QR = 5√2 i |PS|=|DB|=15√2, nie?

Maciess: Tak, to raczej oczywiste. Zaraz wróce do tego zadania i próbuje cos dalej wykombinować

Maciess: Wyliczając wysokość trójkąta QRG opuszczoną na przeciwprostokątną możemy obliczyć długość odcinka |AI'| i mozemy juz z tego policzyć kąt nachylenia przekroju do podstawy

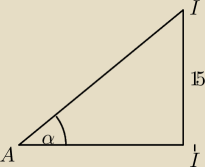
Maciess: Moze ktoś sie pomoze i sprawdzi

	5√2		25√2
|AI'| =15√2−		=
	2		2

	5√86
|AI| z Pitagorasa =
	2

	5√43
cosα=		−−− kąt nachylenia przekroju do podstawy
	86

Wyskość trójkąta APS (oznaczam jako x)

15√2
	/x=cosα tu nie wiem czy dobrze myśle
2

x=3√86

	15√2		1773
|AS|2=(3√86)2+(		)2=
	2		2

	1773		1323
|BS|2=|AS|2−|AB|2=		−225=
	2		2

	21√6
|BS|=
	2

no i wynik inny niz w ksiązce. Ktoś powie co robie nie tak? Rachunkowych raczej nie ma bo liczyłem 2 razy.

Maciess: Może Eta albo Mila pokuszą się o jakieś ciekawe rozwiązanie?

Mila: 352722

Maciess: Czyli se facto tak jak ja (tylko prościej bo ja liczę niepotrzebne cosinusa) i błąd gdzies muszę mieć. Dziękuję za odpowiedź