stereometria hyphaee: Dany jest sześcian ABCDEFGH, którego krawędź ma długość 15. Punkty Q i R dzielą krawędzie HG i FG w stosunku 2:1, to znaczy |HQ|=|FR|=10. Płaszczyzna AQR przecina krawędzie DH i BF odpowiednio w punktach P i S. Oblicz długości odcinków DP i BS.

hyphaee: pomocy

hmm: http://zbior-zadan.pl/oblicz-dlugosc-odcinkow-4?answer=1 https://www.google.pl/search?q=Dany+jest+sze%C5%9Bcian+ABCDEFGH%2C+kt%C3%B3rego+kraw%C4%99d%C5%BA+ma+d%C5%82ugo%C5%9B%C4%87+15.+Punkty+Q+i+R+dziel%C4%85+kraw%C4%99dzie+HG+i+FG+w+stosunku+2%3A1%2C&ie=utf-8&oe=utf-8&client=firefox-b-ab&gfe_rd=cr&ei=bCADWdL0AfKv8wetxKvADg

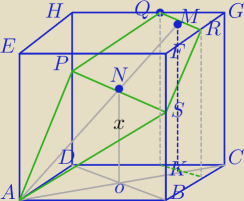
Mila: II sposób. |AC|=15√2 |KC|=2.5√2 |AK|=15√2−2.√2=12.5√2 ΔAKM∼ΔAON

KM		AK
	=
x		AO

15		12.5√2
	=
x		7.5√2

15		125		15		5
	=		⇔		=
x		75		x		3

5x=45 x=9 |DP|=|BS|=9 ==========

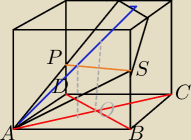g: odkopuje bo nie rozumiem, skad wiadomo,że punkt P nie jest niżej od punktu S?Np. tak jak na tym rysunku,wtedy chyba wysokosc trojkata AON(na rysunku Mili) nie opadałaby na punkt przeciecia przekatnych kwadratu ABCD tylko gdzies blizej wierzcholku A

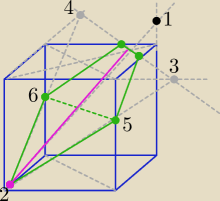Mila: Obejrzyj jak się rysuje przekroje sześcianu− Cabri− Bronisław Pabich. https://cabrigeometry.wordpress.com/2013/01/29/przekroje-szescianu/

g: o fajnie wytlumaczone,ale np. na maturze jak należałoby to zargumentować? przepraszam,że tak susze głowe ale nie daje mi to spokoju

Mila: Nie trzeba uzasadniać, rysunek dobry i liczysz poprawnie.