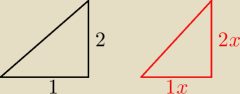
Pytanie co do oznaczeń trygonometrycznych qwerty123: Hej, dajmy przykładowo takie zadanie: Wykaż, że jeżeli α jest kątem ostrym i tgα = 2 to cosα jest liczbą niewymierną Ogólnie zadanie umiem zrobić, ale mam pytanie dotyczące oznaczeń, ponieważ nie chce stracić za to punktów na maturze, jakby jakiś sprawdzający pomyślał, że skąd ja takie coś wziąłem. Mój korepetytor powiedział, że w takim wypadku mogę narysować trójkąt, lecz zamiast takich oznaczeń jak w trójkącie czarnym, powinienem dodawać 'x' (które i tak się zredukują), ponieważ te wartości trygonometryczne nie są dokładne (czy coś takiego, niestety nie pamiętam uzasadnienia) Czy można tak oznaczać jak po prawej + czy błędem jest oznaczanie w taki sposób jak po lewej? Pozdrawiam

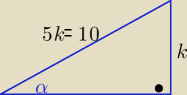
Eta: Szczególnie w taki przypadku :

	1
sinα=
	5

oblicz tgα

xyz: oznaczaj jak po prawej. Rysunek po lewej jest bledny, bo przyprostokatne rownie dobrze moga miec dlugosci 4 i 2, 5 i 5/2, 6 i 3 czy tez 1 i 0,5 itd. Czyli wielokrotnosci 2 i 1, zatem te pomnozenie razy x jest istotne zeby zaznaczyc ze to zachodzi dla trojkatow ktorych boki sa dowolnej dlugosci (przy nadal zachodzacej zaleznosci 2 do 1) a nie tylko dlugosc 2 i 1

qwerty123: ok, dziękuję

6latek: https://matematykaszkolna.pl/forum/388935.html Patrz moj post 9 : 42 Masz tam wyprowadzony wzor na cosinus kata w zaleznosci od tangensa

PW: Nie zgadzam się z przedmówcami jakoby rysunek czarny miał być błędny. Trójkąty czarny i czerwony są podobne. "Przeskalowanie" trójkąta nie zmienia zależności między bokami (w szczególności nie zmienia wartości funkcji trygonometrycznych). Zauważmy, że na tym oparta jest zasada definiowania funkcji trygonometrycznych dowolnego kąta skierowanego. Bierzemy dowolny punkt P=(x, y) na końcowym ramieniu kąta w układzie

	y
współrzędnych i definiujemy np. tgα=		. A co gdy przysłowiowy mały Jasio powie:
	x

− A ja nie rozumiem, jak to "dowolny"? Mówimy mu: − Jasio, przecież ...