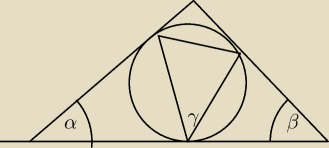
Kąty 6latek: To juz nie wiem Tresc .

	α+β
Pokaz ze γ=
	2

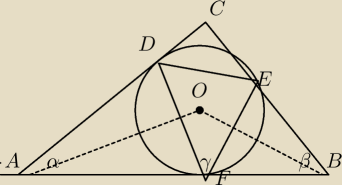
6latek: Srodek tego okregu bedzie lezal na przecieciu sie dwusiecznych Natomiast zeby wpisac ten drugi trojkat srodek na przecieciu sie symetralnych Nic wiecej nie wykombinuje

Leszek: Skorzystaj z twierdzenia o stycznych do okregu , wowczas rozpatrujesz trojkaty rownoramienne przy ktorych sa jednakowe katy : α +2δ₁ = 180° , β= 2δ₂ = 180° Oraz : δ₁ + δ₂ + γ = 180° ⇒ γ =(α +β)/2

6latek: Leszek czyli rozpatruje trojkaty ADF i EFB one sa rownoramienne Nie pomyslaem o tych stycznych dziekuje

an: 6latku, a do czego Ci potrzebna jest ta geometria, wydaje mi się,że powinieneś zająć się czymś innym na pewno znajdziesz zajęcie, z którego będziesz zadowolony i da ci ono jakąś radość, jest takie powiedzenie "z niewolnika nie ma pracownika". POZDRAWIAM an

ite: @an Dlaczego uważasz, że zajęcie, w które się wkłada dużo pracy, nie daje zadowolenia? Przecież to jest dokładnie odwrotnie.

6latek: Witaj an Pewnie cos by sie znalazlo Ucze sie tej geometrii zeby pomoc wnuczce i wnukowi Wnuczka ma 12 lat ,a wnuk bedzie mial teraz 7 lat Pozdrawiam

Mila: Czy D, E, F to punkty styczności okręgu z bokami Δ? Rysunek niedokładny, a żadnej treści nie ma, dlatego pytam

iteRacj@: @Milu możesz spojrzeć na moje rozwiązanie z wątku 388759? Czy są jakieś inne czworokąty spełniające warunki zadania?

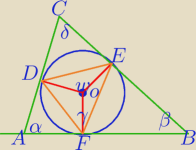
Mila: 1) α+β+δ=180, δ=180−(α+β) 2) δ+w=180 w=180−δ w=180−(180−(α+β)) w=α+β

	α+β
3) γ=
	2

cnw

Wenera: 6latku z ciekawości ośmiele się zapytać. Dlaczego robisz zadania z jakichś dziwnych starych zbiorów? Przygotowujesz się do matury? Od kiedy sięgam pamięcią jesteś całkiem starym użytkownikiem tego forum.

6latek: https://zapodaj.net/dbced479ea2e7.jpg.html Milu zadanie nr 342

6latek: Wenera Bo tylko takie zbiory mam . Z nowszych tylko mam Mizie .