Punkty 6latek: Dane sa niewspolliniowe punkty ABC takie ze AB = BC Znajdz konstrukcyjnie punkt D ze istnieje okrag wpisany w czworokat ABCD i istnieje okrag opisany na tym czworokacie Wydaje mi sie ze tym czworokatem bedzie kwadrat Wiec nalezy skonstruowac punkt symetryczny dla C wzledem prostej AB

ite: Takim czworokątem będzie deltoid o czwartym wierzchołku wyznaczonym przez okrąg opisany na ΔABC. Nie wiem, tak z marszu, czy jeszcze jakiś inny (może ktoś podpowie). Żeby to był kwadrat, to kąt między AB i BC musiałby mieć 90^o, a tego nie ma w treści zadania.

6latek: Dziekuje Sprawdze .

ite: Jeśli mój opis nie jest wystarczający, to zrobię rysunek. Może ktoś jeszcze się wypowie, czy istnieją inne rozwiązania.

Jerzy: AB i CD nie mogą być przekątnymi deltoidu.

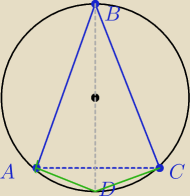
ite: Dane są niewspółliniowe punkty A,B,C takie że |AB|=|BC|. Moja konstrukcja jest taka: 1/ rysuję odcinki AB, BC, AB 2/ rysuję symetralne tych odcinków, znajduję środek okręgu opisanego na ΔABC 3/ przedłużam symetralną boku AB tak żeby przecięła okrąg, wyznaczając pkt D − czwarty wierzchołek szukanego czworokąta Z konstrukcji wynika, że istnieje okrąg opisany na ABCD. BD jest średnicą tego okręgu a |AB|=|BC|, więc również |AD|=|DC|. Stąd |AB|+|DC|=|BC|+|AD| czyli sumy długości przeciwległych boków czworokąta są równe. Więc w ten czworokąt można wpisać okrąg. Chyba wszystko się zgadza ? ?

6latek: Tak ite Zgadza sie . U mnie nie zgadzalyby sie oznaczenia

Mila: ładna konstrukcja.

iteRacj@: Dziękuję!