Konstrukcja
6latek: Skonstruj trapez wpisany w dany okrag majac dane podstawy trapezu
7 kwi 10:52
Jerzy:
Cześć

I gdzie masz problem ?
7 kwi 11:12
6latek: Dzien dobry

No wlasnie w konstrukcji .
Jerzy jesli to bedzie trapez rownoramienny to nie ma problemu bo narysuje os symetrii
Ale mozna tez wpisac rowniez inny trapez niz rownoramienny
7 kwi 11:17
Jerzy:
Jeśli nie jest równoramienny,to zadanie nie ma rozwiązania,bo takich trapezów jest
nieskończenie wiele.
7 kwi 11:22
Jerzy:
I o co chodzi z tą osią symetrii ?
7 kwi 11:22
6latek:
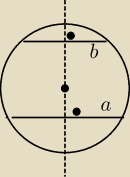
7 kwi 11:26
Jerzy:
To jest wynik, ale teraz opisz konstrukcję

7 kwi 11:27
6latek: Dobrze . Musze sie jeszcze zastanowic
7 kwi 11:31
7 kwi 16:35
Mila:
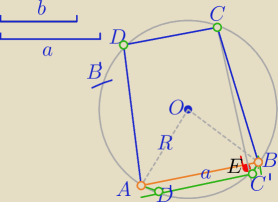
b<a
a≤2R
| | a+b | |
1) konstrukcja odcinka m= |
| |
| | 2 | |
2) rysuję okrąg o(O,R)
3) obieram p.A na okręgu
4) kreślę okrąg o(A,a)⇒otrzymuję pkt. B ( i B')
| | a+b | |
5) kreślę o(A,r= |
| ⇒otrzymuję E− punkt przecięcia z AB |
| | 2 | |
6) Konstrukcja h⊥AB i przechodzącej przez punkt E⇒otrzymuję dwa punkty przecięcia
z okręgiem o(O,R)
7) kreślę równoległe do AB i przechodzące przez C i C'
czworokąty:
ABC'D", ABCD są trapezami wpisanymi w dany okrąg o podstawach odpowiednio: a i b.
Konstrukcja nie jest dokładna, bo trudno tu narysować dokładnie.
W zeszycie wyjdzie .

7 kwi 17:47
6latek: Dzien dobry
Milu 
Dziekuje Ci . Natrudzilas sie duzo .
7 kwi 17:54
Mila:
Dzień dobry.

7 kwi 17:59
 I gdzie masz problem ?
I gdzie masz problem ?
 No wlasnie w konstrukcji .
Jerzy jesli to bedzie trapez rownoramienny to nie ma problemu bo narysuje os symetrii
Ale mozna tez wpisac rowniez inny trapez niz rownoramienny
No wlasnie w konstrukcji .
Jerzy jesli to bedzie trapez rownoramienny to nie ma problemu bo narysuje os symetrii
Ale mozna tez wpisac rowniez inny trapez niz rownoramienny


 b<a
a≤2R
b<a
a≤2R

 Dziekuje Ci . Natrudzilas sie duzo .
Dziekuje Ci . Natrudzilas sie duzo .
