Trapez roworamienny
6latek: Udowodnij ze jesli traz jest wpisany w okrag to jest rownoramienny
Dowod z symetrii osiowej
28 mar 19:08
6latek: Ma byc trapez oczywiscie .
28 mar 19:09
6latek:
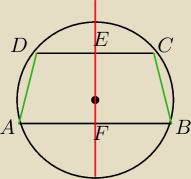
ABIICD
Jesli poprowadzimy prosta prostopadla przechodzaca prze srodek okregu do AB i CD to DE=EC a
takze AF=FB
Teraz jak udowodnic ze ramiona sa rownej dlugosci ?
28 mar 19:22
6latek: Posrednio skorzystalem z twierdzenia ze prosta prostopadla do cieciwy dzieli ja na polowy
28 mar 19:24
28 mar 19:36
6latek:
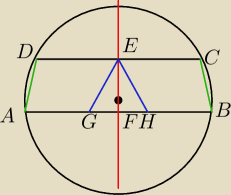
Jeszcze jest jedna rzecz
Prosta przechodzaca przez srodek okregu jest jego osia symetrii a symetria osiowa zachowuje
odleglosc punktow
Wiec raczej chyba z tego ronosc odcinkow DEi Ec a takze AF i FB
Teraz jezeli z punktu E wyprowadze rownolegla do BC i AD to mam dwa rownolegloboki
ADEG i HBCE
Stad mam ze AD=EG i CB=EH
Ale tez skoro EF jest osia symetrii to trojkat EGH jest rownoramienny stad EH=EG i stad
wniosek ze AD=CB
Moze tak byc ?
28 mar 19:50
6latek: Dobry wieczor
PW 
dziekuje . Pisalem i nie zauwazylem Twojego wpisu
28 mar 19:52
PW: 
28 mar 19:56
6latek: To mnie zasmuciles

Napisz prosze co jest zlego w moim dowodzie
mam to zadanie w paragrafie z symetrii osiowej
28 mar 20:04
PW: Wiec raczej chyba z tego ronosc odcinkow DEi Ec a takze AF i FB − to nie jest prawda. Wystarczy
narysować tę czerwoną prostą pod innyn kątem do podstaw.
28 mar 20:09
6latek: Wiec co nalezaloby napisac ?
28 mar 20:12
PW: Nie upieram się, że mój dowód jest "jedyny słuszny", ale zwróć uwagę, że biorę symetralną
odcinka AB, symetralną odcinka DC i pokazuję, że obie symetralne pokrywają się. Wtedy symetria
o osi k załatwia sprawę równości |BC| i |AC|
28 mar 20:19
6latek: Dobrze .
Wiesz duzo mi sie teraz klebi w glowie chocby to ze z definicji trapezu mamy jedna pare
bokow rownoleglych
Natomiast dwie proste sa rownolegle jesli sa prostopadle do trzeciej prostej
28 mar 20:30
6latek: Moze ktos spojrzy i napisze dowod
29 mar 07:26
29 mar 08:43
6latek: dzieki. zapoznam sie
29 mar 08:52
a7:
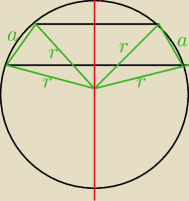
symetralna podstaw przechdzi przez środek okeęgu i mamy dwa trójkąty równoramienne o tych
samych katach o bokach r więc podstawy też będą równe
29 mar 08:55
a7: 
29 mar 08:55
ite:
@a7 pytasz, czy dowód, który wpisałaś jest poprawny?
29 mar 09:16
a7: @ite tak,
29 mar 10:05
29 mar 10:16
a7:
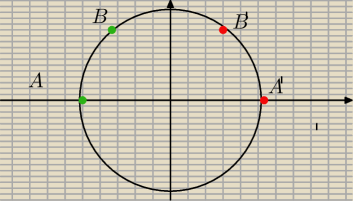
jeśli chodzi o dowód z symetrii osiowej to bierzemy okrąg w układzie wspólrzędnych o robimy
symetrię osiową punktu A i B i mierzymy długości odcinków AB i A'B'
i mamy dowód np. A(−x,0) B(−x+1,r−1) itd. ....

29 mar 10:25
ite:
8:55 Musisz wskazać, które kąty są równe i dlaczego.
29 mar 10:26
a7:
A'=(x,0) B'=(x−1, r−1)
|AB|=|A'B'|
c.n.w.
29 mar 10:27
ite:
10:25 Dowód ma pokazać prawdziwość tezy dla każdych punktów A i B, a nie tylko tych
"pomierzonych".
Jak piszesz o symetrii osiowej, to musisz podać względem jakiej osi przekształcasz.
29 mar 10:30
a7:
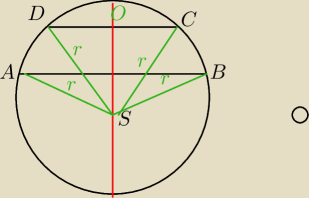
@ite kąty trójkąt DCS i trójkąt ASB są równoramienne − SO jest jego symetralną i osią symetrii
i wysokością itd więc
kąty OSA i OSB odjąć odpowiednio kąty OSD i OSC są równe więc mamy |AD|=|CB| c.n.w.

29 mar 10:34
a7: do dowodu z 10:27 oczywiście używamy wzoru na długość odcinka w układzie współrzędnych
29 mar 10:36
a7:
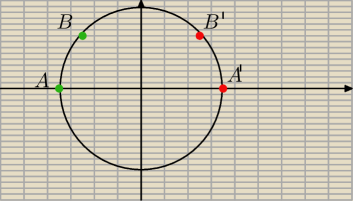
A=(−x,y) A'=(x,y) r − promień okręgu
B=(−x+a, r−b) a>0 b<r (?) B'=(x−a, r−b)
|AB|=
√(−a)2 , (y−r+b)2
|A'B'|=
√a2, (y−r+b)2
|AB|=|A'B| c.n.w.
29 mar 10:49
ite:
10:34
Jak wykazałaś równość kątów, to dalej przystawanie trójkątów (z podaniem na podstawie której
własności). I dopiero z cech trójkątów przystających wynika równość odcinków AD i BC.
29 mar 10:58
a7: w takim razie uzupełniam jeszcze , że trójkąty te (ΔABS,ΔDCS)są podobne − przystające z cechy
b,k,b
29 mar 11:09
a7: a skoro są przystające to i boki AD i CB muszą być równe
teraz ok?
29 mar 11:11
ite: Nie, ponieważ trzeba określić, czy się wykazuje podobieństwo czy przystawanie : )
Nie może chodzić o ΔABS, ΔDCS − nie są podobne. Pewnie mają być pary ΔDOS i ΔCOS oraz ΔAO'S i
ΔBO'S.
29 mar 11:17
a7: założenia na a i b też do korekcji

, ale też nie jestem pewna a < r i b<2r ?
29 mar 11:19
a7: ok poddaję się
29 mar 11:20
a7: myślę, że ten dowód w linku 10:16 jest ok, oraz dowód 10:49 może można zaliczyć jako dowód z
symetrii osiowej

29 mar 11:21
ite:
Jeśli 10:49 ma wynikać z symetrii osiowej, to musisz podać względem jakiej osi jest symetria i
który punkt jest obrazem którego.
29 mar 11:46
a7: symetria jest względem osi OY i oczywiście A' jest obrazem puntu A i odpowiednio B' obrazem
punktu B

29 mar 11:52
ite:
To dalej trzeba by pokazać, że BB' jest równoległe do AA' ← to ma być trapez.
Ale i tak to musiałabyś zmienić położenie drugiej podstawy. Teraz dowodzisz tezę tylko dla
szczególnej sytuacji: jedna z podstaw trapezu jest średnicą opisanego na nim okręgu!
29 mar 12:02
a7: nie tylko gdy jest średnicą 10:49 uogólniłam zapis
29 mar 12:03
a7: to że AA' jeat równoległe do BB' wynika z ich współrzędnych ( przeciwna współrzędna "iksowa",
ta sama "ygrekowa")
29 mar 12:06
ite:
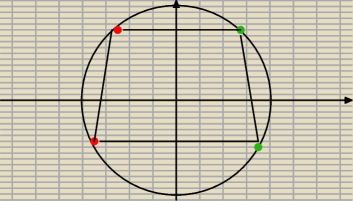
10:49 ← w ten sposób nie opiszesz prostokąta, a też jest trapezem
29 mar 12:10
a7: ale to by już było inne zagadnienie
jeden z punktów A i odpowiednio dobrany punkt B byłby już prostokątem , ale to jest już inne
zagadnienie
29 mar 12:15
a7:
29 mar 12:18
Jerzy:
Nie przeprowadza się w geometrii dowodów, wykorzystując współrzedne punktów.
To nie jest geometria analityczna.
29 mar 12:22
a7: ok, w takim razie sorry za zaśmiecenie forum
29 mar 12:26
ite: @Jerzy Dlaczego tak nie można ?
W "Informatorze o egzaminie maturalnym z matematyki od roku szkolnego 2014/2015" wśród
przykładowych rozwiązań w zadaniu "Wykaż, że .." CKE podaje:
Sposób III (geometria analityczna)
Rozwiązanie zadania sposobem analitycznym składa się z trzech kroków. Po pierwsze,
w wygodny sposób umieszczamy rozważane figury geometryczne w układzie współrzędnych
lub równoważnie do istniejących figur dobieramy układ współrzędnych. Po drugie,
w przyjętym układzie współrzędnych obliczamy współrzędne potrzebnych punktów.
Wreszcie, za pomocą obliczonych współrzędnych, obliczamy wielkości, o które chodzi
w zadaniu.
29 mar 13:58
Jerzy:
No , jeśli CKE tak twierdzi, to nie mam nic do dodania.
29 mar 14:02
6latek: Przepraszam wszystkich ze w tym czasie dyskusji spalem

29 mar 17:09
ABC:
kto śpi ten nie grzeszy

29 mar 17:11
6latek: Witam

Jednak w tym temacie przychyle sie do dowodu
PW
Wydaje sie najprostszy wedlug mnie . tak mi sie śniło

29 mar 17:13
a7: 
29 mar 17:58
6latek: Dobry wieczor

Czy Ty nie jestes czasami
Aga1 (jesli wolno mi zapytac ?
29 mar 18:54
a7: Dobry wieczór, nie to mój pierwszy nick
30 mar 21:15
6latek: OK

Dobranoc

31 mar 00:33
 ABIICD
Jesli poprowadzimy prosta prostopadla przechodzaca prze srodek okregu do AB i CD to DE=EC a
takze AF=FB
Teraz jak udowodnic ze ramiona sa rownej dlugosci ?
ABIICD
Jesli poprowadzimy prosta prostopadla przechodzaca prze srodek okregu do AB i CD to DE=EC a
takze AF=FB
Teraz jak udowodnic ze ramiona sa rownej dlugosci ?
 Jeszcze jest jedna rzecz
Prosta przechodzaca przez srodek okregu jest jego osia symetrii a symetria osiowa zachowuje
odleglosc punktow
Wiec raczej chyba z tego ronosc odcinkow DEi Ec a takze AF i FB
Teraz jezeli z punktu E wyprowadze rownolegla do BC i AD to mam dwa rownolegloboki
ADEG i HBCE
Stad mam ze AD=EG i CB=EH
Ale tez skoro EF jest osia symetrii to trojkat EGH jest rownoramienny stad EH=EG i stad
wniosek ze AD=CB
Moze tak byc ?
Jeszcze jest jedna rzecz
Prosta przechodzaca przez srodek okregu jest jego osia symetrii a symetria osiowa zachowuje
odleglosc punktow
Wiec raczej chyba z tego ronosc odcinkow DEi Ec a takze AF i FB
Teraz jezeli z punktu E wyprowadze rownolegla do BC i AD to mam dwa rownolegloboki
ADEG i HBCE
Stad mam ze AD=EG i CB=EH
Ale tez skoro EF jest osia symetrii to trojkat EGH jest rownoramienny stad EH=EG i stad
wniosek ze AD=CB
Moze tak byc ?
 dziekuje . Pisalem i nie zauwazylem Twojego wpisu
dziekuje . Pisalem i nie zauwazylem Twojego wpisu

 Napisz prosze co jest zlego w moim dowodzie
mam to zadanie w paragrafie z symetrii osiowej
Napisz prosze co jest zlego w moim dowodzie
mam to zadanie w paragrafie z symetrii osiowej
 symetralna podstaw przechdzi przez środek okeęgu i mamy dwa trójkąty równoramienne o tych
samych katach o bokach r więc podstawy też będą równe
symetralna podstaw przechdzi przez środek okeęgu i mamy dwa trójkąty równoramienne o tych
samych katach o bokach r więc podstawy też będą równe

 jeśli chodzi o dowód z symetrii osiowej to bierzemy okrąg w układzie wspólrzędnych o robimy
symetrię osiową punktu A i B i mierzymy długości odcinków AB i A'B'
i mamy dowód np. A(−x,0) B(−x+1,r−1) itd. ....
jeśli chodzi o dowód z symetrii osiowej to bierzemy okrąg w układzie wspólrzędnych o robimy
symetrię osiową punktu A i B i mierzymy długości odcinków AB i A'B'
i mamy dowód np. A(−x,0) B(−x+1,r−1) itd. ....

 @ite kąty trójkąt DCS i trójkąt ASB są równoramienne − SO jest jego symetralną i osią symetrii
i wysokością itd więc
kąty OSA i OSB odjąć odpowiednio kąty OSD i OSC są równe więc mamy |AD|=|CB| c.n.w.
@ite kąty trójkąt DCS i trójkąt ASB są równoramienne − SO jest jego symetralną i osią symetrii
i wysokością itd więc
kąty OSA i OSB odjąć odpowiednio kąty OSD i OSC są równe więc mamy |AD|=|CB| c.n.w.

 A=(−x,y) A'=(x,y) r − promień okręgu
B=(−x+a, r−b) a>0 b<r (?) B'=(x−a, r−b)
|AB|=√(−a)2 , (y−r+b)2
|A'B'|=√a2, (y−r+b)2
|AB|=|A'B| c.n.w.
A=(−x,y) A'=(x,y) r − promień okręgu
B=(−x+a, r−b) a>0 b<r (?) B'=(x−a, r−b)
|AB|=√(−a)2 , (y−r+b)2
|A'B'|=√a2, (y−r+b)2
|AB|=|A'B| c.n.w.
 , ale też nie jestem pewna a < r i b<2r ?
, ale też nie jestem pewna a < r i b<2r ?





 Jednak w tym temacie przychyle sie do dowodu PW
Wydaje sie najprostszy wedlug mnie . tak mi sie śniło
Jednak w tym temacie przychyle sie do dowodu PW
Wydaje sie najprostszy wedlug mnie . tak mi sie śniło 

 Czy Ty nie jestes czasami Aga1 (jesli wolno mi zapytac ?
Czy Ty nie jestes czasami Aga1 (jesli wolno mi zapytac ?
 Dobranoc
Dobranoc 