? Rajstopy: Czy każdy trapez wpisany w okrąg jest równoramienny ? Jak tak to dlaczego ?: P

PW: Wynika to np. z własności symetrii osiowej, Bierzemy symetrię o osi k prostopadłej do podstawy AB, przechodzącej przez środek okręgu. Przekształcamy za pomocą tej symetrii wierzchołek C. Wiesz jak dalej argumentować?

Rajstopy: nie bardzo próbowałam coś z kątami itd. symetria to moja słaba strona

J: W okrąg można wpisać czworokąt tylko wtedy, gdy sumy przeciwległych kątów są równe, zatem .... trapez musi być równoramienny

Eta: dla J

J: Witaj Eta , ... a dla Ciebie cały kosz

PW: Symetria ta przekształca okrąg na ten sam okrąg (bo oś przechodzi przez środek okręgu − korzystamy ze znanego twierdzenia), wobec tego obrazem punktu C jest leżący po przeciwnej stronie prostej pewien punkt C' należący do okręgu, a obrazem B jest A i na odwrót. Jednocześnie obrazem prostej CD prostopadłej do k jest ta sama prosta CD. Wniosek: C' = D (wynika to z faktu, że prosta i okrąg mają co najwyżej dwa punkty wspólne). Pokazaliśmy, że obrazem odcinka BC jest odcinek AD, To oznacza, że |BC| = |AD|, gdyż symetria osiowa jest izometrią (odległość obrazów jest równa odległości przekształcanych punktów). Być może jest dowód łatwiejszy, bywa że komplikuję proste sprawy,

PW: Niech trapez ma kąty α, β, γ, δ. Czy z tego że α + γ = β + δ wynika w sposób oczywisty coś o bokach trapezu? Znowu mnie nie przekonałaś. Może dzisiaj marudny jestem

PW: Oj, przepraszam, przypisałem wypowiedź Ecie, a nie J.

J: Tylko w trapezie równoramiennym sumy przeciwległych kątów równe

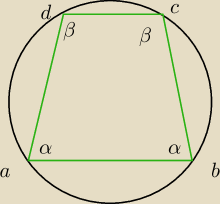
Rajstopy: β = 180 STOPNI − α teraz suma kata a + kata c = 190 STOPNI czyli kat C ma bete aha czyli kat B ma alfe czyli trapez jest równoraminney

J: o to chodzi ... α + β = α + β

PW: Zgodzę się, jeżeli podasz dowód − Rajstopy chciała uzasadnienia.

J: Pokaż trapez, który ma sumy równe, a nie jest równoramienny

PW: J, zlituj się, to miał być dowód. Mówicie o kątach, a nie o długościach boków.

J: Trapez można wpisać w okrąg wtedy i tylko wtedy, gdy jest trapezem równoramiennym. .... przyjmij to do wiadomości

Rajstopy: Niweeeeee już bardziej nie chcę Tyle wystarczy J dobrze mnie naprowadziłeś W ksiazce mam napisane ze trapez jest równoramienny jezeli ma katy przy podstawie te same i jak juz to pokazałam tak jak ty pisałes to zgodnie z definicja uznaje to za zakończone PW także tb dziekuje ale tak dokładnie jak TY nie chciuałam bo nie walcze o 5

PW: Pozostaję niepocieszony. Ja wiem, że jestem zgryźliwy, ale dowody polegające na pokrzykiwaniu typu "przyjmij to do wiadomości" już w dzieciństwie mnie nie przekonywały. Rajstopy, niczego nie pokazałaś, co świadczyłoby o równości ramion trapezu. Spojrzyj trzeźwo − cały czas piszesz o kątach i na tym skończyłaś. Ani słowem nie wspomniałaś o równoległości podstaw trapezu. Przecież to co napisałaś można powiedzieć o każdym czworokącie wpisanym w okrąg, i żadne wnioski o długościach boków z tego nie wynikają. Już więcej nie wypowiadam się na ten temat, żebyście nie pomyśleli że koniecznie muszę mieć rację

J: PW .. .nikt nie powiedział,że nie masz racji .... masz , tylko pytanie było, czy trapez musi być równoramienny ... odpowiedź: TAK

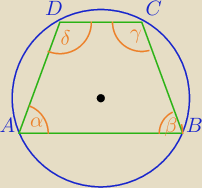
Mila: AB||CD⇔ABCD jest trapezem⇔Suma miar kątów przy ramieniu jest równa 180^o. α+δ=180^o β+γ=180⇔γ=180−β ABCD jest czworokątem wpisanym w okrąg⇔ α+γ=180 i β+δ=180 α+180−β=180⇔ α−β=0 α=β kąty przy podstawie są równe ⇔ten trapez jest trapezem równoramiennym.