Ekstrema pierzyna: Jak to jest z tymi ekstremami? Dotychczas widząc na maturach zadania typu "udowodnij, że prawdziwa jest nierówność (przykładowo) x⁴+6x²+12≥0" od razu na brałem się za udowodnienie, że minimum lokalne funkcji będzie większe bądź równe 0, czym udowodnię nierówność. Jednak ostatnio miałem maturę próbną w szkole, w której zrobiłem dokładnie tak, jak robiłem od zawsze, a opisałem powyżej, i dostałem za taki dowód 2/3 punkty. Na czerwono nauczycielka narysowała mi tabelę opisującą przebieg monotoniczności funkcji i pochodnej − moje zapisanie warunku koniecznego na istnienie ekstremum jej nie wystarczyło... Jak to w końcu jest z tym obliczaniem minimalnych wartości funkcji? Jeżeli funkcja ma jedne i jedyne minimum lokalne w dziedzinie, to nie oznacza to, że przyjmie wartość najmniejszą dla tego minimum?

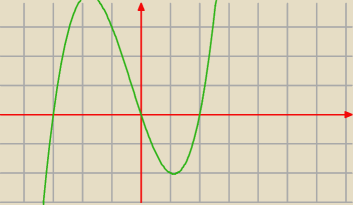
ABC: a ty znowu swoje.... ta funkcja ma jedno minimum lokalne i jedno maksimum w swej dziedzinie i nie są to wartości największe ani najmniejsze globalnie

pierzyna: @ABC zatem jeśli masz chęci i umiejętności − wytłumacz mi Z tego co piszesz zrozumiałem tyle, że tak naprawdę obliczanie minimów lokalnych jest w takich zadaniach bezużyteczne, bo nie jest w stanie ujawnić minimalnej wartości przyjmowanej przez funkcję. A przecież taki sposób jest nawet w kluczu.

ABC: wczoraj ci Blee zrobił cały wykład o tym tutaj .... https://matematykaszkolna.pl/forum/388440.html nie mówię że jest bezużyteczne ale przeważnie potrzebujesz dodatkowych informacji o funkcji, w nielicznych przypadkach jak wielomian drugiego stopnia i parabola możesz przejść od lokalnego do globalnego bez dodatkowych informacji

pierzyna: @ABC "Udowodnij, że x⁴−2x³−2x²+8" − https://imgur.com/a/DiAwI18 W takim razie taki sposób rozwiązania nie jest w pełni merytorycznie poprawny? Bowiem autor klucza zapisał wyłącznie warunek konieczny do istnienia ekstrema funkcji, nie obliczał żadnych granic, "nie rachował".

ABC: autor pisze prawdę, wykorzystując w sposob ukryty granice w −∞ i +∞ wielomianu parzystego stopnia (4) o dodatnim współczynniku i nie informując o tym czytelnika

pierzyna: @ABC A mógłbyś wyjaśnić w jaki sposób, przy pomocy tych granic, można sprawdzić, czy minimum lokalne jest także i globalne?

ABC: chodzi ci o to konkretne zadanie?

pierzyna: A będą jakieś różnice? Jakie/względem czego?

ABC: względem postaci funkcji, czy to wielomian, funkcja wymierna, wykładnicza, logarytmiczna itp.

ABC: z tych co wymieniłem najgorsze są wymierne, "dziury" w dziedzinie powodują że trzeba bardzo uważać z globalnymi

pierzyna: No ok, to jak będą wyglądać te granice w przypadku wielomianów i funkcji wymiernych?

ABC: wydaje mi się że na tej stronie w jakimś kompendium powinno to być napisane

pierzyna: @ABC po pierwsze, czy w ogóle jest możliwe, żeby granica jakiegokolwiek wielomianu dążyła do czegoś innego niż + i − nieskonczoność?

ABC: Tak

pierzyna: Aha

ABC: Funkcja stała jest wielomianem stopnia zerowego ( oprócz funkcji stale równej zero, bo dla tej w szkole stopnia się nie określa, a w wyższej matematyce czasem przyjmujemy stopień −∞)

PW: O czym dyskutujecie? pierzyna na siłę stwarza problemy, chyba żeby drażnić normalnie myślących uczestników forum. Daje taki "naprzykład": Udowodnić, że prawdziwa jest nierówność x⁴+6x²+12≥0 i opowiada, jak to "od razu brał się za pokazanie minimum lokalnego". A normalnie myślący powie: K..., przecież lewa strona nierówności jest równa co najmniej 12 − co tu dowodzić?".

pierzyna: @PW Normalnie myślący człowiek zrozumie, że skoro temat jest o rozwiązywaniu przy pomocy pochodnej, to chwilowo nie obchodzą mnie żadne inne sposoby. Najwidoczniej ty, mimo jakże długiego stażu, obracaniu się w środowisku matematycznym, wciąż nie dysponujesz na tyle rozwiniętą umiejętnością czytania ze zrozumieniem, by nie zaśmiecać moich tematów bezsensownymi postami, a zdarzyło ci się to już po raz drugi. A co do tematu, to wydaje mi się, że sam już doszedłem do tego o co w tym wszystkim chodzi. Otóż w tego typu dowodach algebraicznych, wielomiany zawsze są stopnia parzystego, bo tylko wtedy da się za pomocą granic i pochodnej udowodnić "globalność" danego minima/maxima. (np. jeśli współczynnik przy najwyższej potędze >0, to lim x−−>+−∞ =+∞)

ICSP:

ABC:

ite: Nauczycielom trzeba przyznać dodatkowe podwyżki za pracę z uczniami, których nie obchodzą żadne inne sposoby (poza 15:54) !

pierzyna: @ite Sposób z sumą kwadratów jest mi bardzo dobrze znany. To sposób z pochodną sprawiał mi problem. Chcę sprawnie posługiwać się więcej niż jednym sposobem. Skoro założyłem temat o sposobie z pochodną, to jednak chciałbym dowiedzieć się o sposobie z pochodną, nie o tym, że 2+2>0, zwłaszcza przedstawione takim tonem.

wredulus_pospolitus: to po co założyłeś drugi temat, skoro w pierwszym (poniedziałek) wyjaśnione Ci zostało co musi zostać wyznaczone aby mieć pełny dowód.

pierzyna: @wredulus_pospolitus Miałem wątpliwości i pytania co do tego wyjaśnienia, dlatego założyłem nowy temat. Chyba od tego jest to forum? Poza tym to nie był mój temat, w zasadzie, to początkowo dotyczył czego innego.

Ateusz: Tak szczerze to troche z Pana buc... PW Najnormalniej na tym forum zachowuja sie Mila i Eta

PW: Wiesz, że na niektórych forach za taką arogancką uwagę o "czytaniu ze zrozumieniem" mógłbyś być wykluczony? Kompromitujesz się. O rozwiązywaniu rzeczy banalnych za pomocą skomplikowanych metod mówi się: − Hebluj, synu, hebluj. Przyjdą ociec, to siekierką poprawią.

PW: Teraz się nazywasz Ateusz? Lecz się, człowieku. Nie recenzuj innych uczestników, bo za chwile możesz tak dostać w kość, że się usmarkasz.

wredulus_pospolitus: Skoro PW to buc ... to kim jak jestem Ale odchodzimy od tematu, a samego tematu w sumie nie ma bo ... zostało to w poniedziałek wyjaśnione −−− należy sprawdzić wartość funkcji w minimach lokalnych + obliczyć granice w ±∞

wredulus_pospolitus: I koniec tematu.

pierzyna: @PW O zgrozo... Człowiek zaczynający swoją "pomoc" w temacie od słów "pierzyna na siłę stwarza problemy, chyba żeby drażnić normalnie myślących uczestników forum.", a kończący "Nie recenzuj innych uczestników, bo za chwile możesz tak dostać w kość, że się usmarkasz." mówi coś o arogancji... @wredulus_pospolitus Najwyraźniej kimś, kto zaczął pisać ten post przed 17:15... Co do jednego pełna zgoda, temat wyjaśniony.