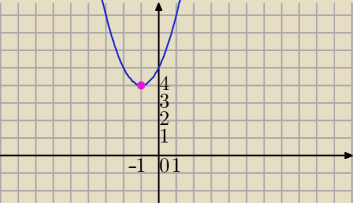
funkcja kw. Paweł: , Wykresem funkcji f(x)=x²+bx+c jest parabola o wierzchołku (−1,4). Oblicz wartości b i c Pomocy, powie kto jak w ogóle się za to zabrać? Jak mniemam sprowadzamy to do postaci kanonicznej, ale "a" tutaj jest chyba 0, więc: f(−1)=0(x+1)² + 4 to mi trochę nie pasuje, bo wtedy wychodz f(x)=4? ktoś coś?

ABC: co naprowadziło cię na koncepcję że a=0 ?

Paweł: w poleceniu przy x² nie ma żadnej innej liczby, więc a = 0?

iteRacj@: f(x)=1*x²+bx+c

ABC: uczyli cię kiedyś co jest elementem neutralnym mnożenia?

Mila:

	−b
a=1, xw=
	2a

=============

	−b
xw=−1⇔		=−1
	2*1

b=2 f(−1)=4 (−1)²+2*(−1)+C=4 c=5 f(x)=x²+2x+5

ABC: Iteracja zaburzyłaś mi metodę Sokratesa

a7: https://matematykaszkolna.pl/strona/79.html a=1

	−b		−b
xw=		podstawiamy −1=		wychodzi b=2
	2a		2

	−Δ		−b2−4ac
yw=		podstawiamy 4=		wychodzi c=......
	4a		4a

Paweł: Ciężko w to uwierzyć, ale tak wyglądało moje pierwotne rozwiązanie jak podaje Mila, ba, sam wyznaczyłem nawet zbiór wartości ale nie chciało mi się wierzyć, że mogłem to dobrze zrobić i zacząłem na siłę szukać błędu w rozwiązaniu i wymyśliłem sobie, że a = 0. muszę chyba zacząć sam sobie ufać w tym co robię!

Eta: Z postaci kanonicznej y=(x+1)²+4 y=x²+2x+5 a=1 ,b=2, c=5 i po ptokach

iteRacj@: @ABC pisząc, nie widziałam Twojego wpisu. A pomysł, że a=0 poruszył mnie oryginalnością.