Współrzędne wierzchołków trójkąta. xyz: Punkt A = (− 1,− 7) jest wierzchołkiem trójkąta równoramiennego ABC , w którym |AC | = |BC | . Obie współrzędne wierzchołka B są liczbami dodatnimi. Okrąg wpisany w trójkąt ABC ma równanie x² + y² = 10 . Oblicz współrzędne wierzchołków B i C tego trójkąta.

Eta: https://matematykaszkolna.pl/forum/388354.html Co jeszcze chcesz? Napisać Ci to w zeszycie?

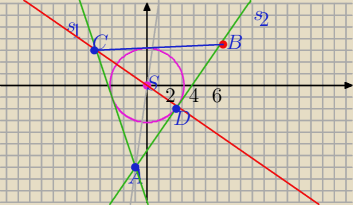
Mila: A = (− 1,− 7) 1) prosta AS: y=7x 2) prosta AC− styczna do okręgu s_ac: y=ax+b, −7=−a+b, b=a−7 y=ax+a−7⇔ax−y+a−7=0 3) Odległość S(0,0) od stycznej jest równa r=√10

|a*0−0+a−7|
	=√10
√a2+1

|a−7|=√10*√a¹+1 /² a²−14a+49=10a²+10

	13
9a2+14a−49=0⇔a=−3 lub a=
	9

	13		50
s1: y=−3x−10 lub s2: y=		x−
	9		9

4) Na prostej s₁ leży punkt C , na prostej s₂ leży punkt B. AB− podstawa Δrównoramiennego CD− wysokość Δ opuszczona AB SD⊥AB (s₂) prosta SD:

	9
y=−		x
	13

5) Punkt D:

13		50		9
	x−		=−		x
9		9		13

	13		9
D=(		,−		)
	5		5

================ Punkt C

	9
−		x=−3x−10
	13

	13
C=(−		,3)
	3

============ 6) Punkt B: D jest środkiem AB⇔

13		−1+xB		9		−7+yB
	=		i −		=
5		2		5		2

	31		17
B=(		,		)
	5		5

============= Posprawdzaj rachunki

Eta: Jak zwykle.... "nadgorliwa" Mila