Geometria analityczna 2415: Punkt A = (− 1,− 7) jest wierzchołkiem trójkąta równoramiennego ABC , w którym |AC | = |BC | . Obie współrzędne wierzchołka B są liczbami dodatnimi. Okrąg wpisany w trójkąt ABC ma równanie x² + y² = 10 . Oblicz współrzędne wierzchołków B i C tego trójkąta.

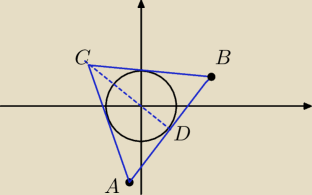
iteRacj@: |AC| = |BC| ⇒ wysokość CD jest też symetralną boku AB D=(x_D,y_D) jest środkiem boku AB

xA+xB
	=xD
2

yA+yB
	=yD
2

D należy do prostej AB stycznej do okręgu równanie tej stycznej → x*x_D+y*y_D=10 [ podziękowania dla autorki tego wzoru ] należy do niej pkt A = (− 1,− 7) otrzymujemy −1*x_D−7*y_D=10 D również należy do okręgu, więc x_D²+y_D²=10.

	9
Rozwiązaniami tego układu równań są x1=1 i x2=		.
	5

I tu mam pytanie, czy rzeczywiście są dwa możliwe położenia punktów D i B, czy ja gdzieś popełniam błąd w obliczeniach?

ABC: Iteracja nie popełniasz błędu w obliczeniach, gdybyś pomyślała o tym że zamieniając oznaczenia B z C wszystkie rozważania pozostają w mocy to byś zajarzyła że muszą być dwie styczne

iteRacj@: Myślę, myślę i to w każdą stronę! Ale nie mogę zamienić B z C, bo "Obie współrzędne wierzchołka B są liczbami dodatnimi." ? ? ?

ABC: i to jest właśnie dodatkowy warunek który pozwoli ci wyeliminować jedno rozwiązanie

iteRacj@: I wszystko się zgadza! Dziękuję

Eta:

ABC:

iteRacj@: 18:17 zgubiłam minusy i zamieniłam nazwy, poprawiam gdyby ktoś chciał z tej odpowiedzi skorzystać.

	−9
Rozwiązaniami tego układu równań są yD1=−1 i yD2=		.
	5

	13		−9
Tylko D=(		;		) daje poprawny wynik dla B=(6,2; 3,4) /obie współrzędne dodatnie/.
	5		5

	1
Wtedy C=(−4		; 3)
	3