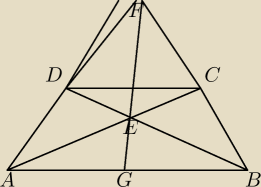
 PΔADE=PΔBEC, gdyż PΔ ADB=PΔ ACB (mają współna podstawę i wysokość) odjąć PΔAEB
PΔAEG=PΔBEG ponieważ te trójkąty mają wspólną wysokość a ich pola są równe (gdyż są równe
PΔADB−PΔAED) to prosta FE musi dzielić podstawę na dwa równe odcinki
PΔADE=PΔBEC, gdyż PΔ ADB=PΔ ACB (mają współna podstawę i wysokość) odjąć PΔAEB
PΔAEG=PΔBEG ponieważ te trójkąty mają wspólną wysokość a ich pola są równe (gdyż są równe
PΔADB−PΔAED) to prosta FE musi dzielić podstawę na dwa równe odcinki
 Tam masz b. ładny sposób.
Może to będzie łatwiejsze? Dłuższy sposób.
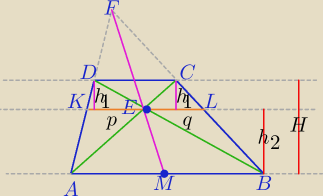
KL||AB, KL||DC
1) Wykażemy, że |KE|=|LE|
PΔADE=PBEC ( to jest wiadome? i oczywiste?)
Tam masz b. ładny sposób.
Może to będzie łatwiejsze? Dłuższy sposób.
KL||AB, KL||DC
1) Wykażemy, że |KE|=|LE|
PΔADE=PBEC ( to jest wiadome? i oczywiste?)
| 1 | 1 | 1 | 1 | |||||
PΔADE= | *p*h1+ | p*h2= | p*(h1+h2)= | p*H | ||||
| 2 | 2 | 2 | 2 |
| 1 | ||
PΔBEC= | q*H⇔ | |
| 2 |
| 1 | 1 | ||
p*H= | q*H⇔ | ||
| 2 | 2 |
| |KE| | |AM | |||
2) ΔFKE∼ΔFAM⇔ | = | ⇔|KE|*|FM|=|FE|*|AM| | ||
| |FE| | |FM| |
| LE | MB | |||
ΔFLE∼ΔFBM⇔ | = | ⇔|LE|*|FM|=|FE|*|MB| | ||
| FE | FM |
| |KE| | |AM| | ||
=1= | ⇔ | ||
| LE | |MB| |
 trudne zadanie chyba
trudne zadanie chyba