stereo Ateusz: Dany jest sześcian ABCDEFGH. Przez wierzchołki A i C oraz środek K krawędzi BF poprowadzono płaszczyznę, która przecina przekątną BH w punkcie P (zobacz rysunek). rysunek : https://matematykaszkolna.pl/strona/4743.gif

iteRacj@: czy o coś w związku z tym pytasz : ))

Ateusz: Owszem : Od czego zacząć? Co potem? Z jakich własności skorzystać? Co powinienem zauważyć?

Ateusz: * Wykaż, że BP:HP=1:3

Ateusz: A jeżeli chodzi o rysunek, to w maturze podany był tylko ten pierwszy.

iteRacj@: Musisz wyobrazić sobie położenie pkt P względem podstawy sześcianu. Dlatego trzeba narysować przekrój zawierający przekątną BH czyli ten drugi rysunek.

Ateusz: Tylko, że z tamtego objaśnienia nie rozumiem pare istotnych rzeczy między innymi, skąd pewność, że KS przechodzi przez P?

iteRacj@: Jest to przekrój, w którym możesz wyrazić (z pomocą boku sześcianu) długości większości odcinków. Szukasz zależności (podobieństwo, przystawanie), w których dzięki znanym odcinkom dasz radę wyrazić długość tych występujących w poleceniu.

iteRacj@: skąd pewność, że KS przechodzi przez P? płaszczyzna HFDB dzieli sześcian dwie przystające bryły

iteRacj@: Pkt S jest punktem wspólnym półprostej KP i podstawy, a ze względu na symetryczność sześcianu lezy na środku odcinka AC.

iteRacj@: A przekątne kwadratu (czyli podstawy sześcianu) przecinają się w punkcie, który jest środkiem ich obu, czyli również środkiem DB.

Ateusz: nie wiem, jakos trudno mi to sobie wyobrazic, "fakty" mi sie nie łączą tak łatwo jak np. tobie po prostu tego jakos nie widze, a identycznych zadanek jest sporo na maturach, wiec bede musial chyba wkuc schemat wykonywania na pamiec...

Ateusz: @iteRacj@ a mógłbyś mi to tak schludnie narysować w rzucie takim, że będzie widać dokładnie i te ważne trójkąty stworzone przez płaszczyznę i sam sześcian?

iteRacj@: A czy taki w ogóle jakiś jeden schemat istnieje? No i jeszcze o ile pamiętam, to nowa matura (2015) miała być taka, żeby zadania były nieschematyczne. Może na ruchomym modelu będzie łatwiej zobaczyć symetrię. Można go przekręcić np. do góry nogami. https://www.geogebra.org/3d/mysutxmn

Ateusz: przejrzalem na oczy dzieki

Ateusz: ale niestety, na maturce takich podglądów nie będę miał pewnie szansy stworzyć

iteRacj@: To twórz takie modele, ucząc się. To poprawia wyobraźnię i pozwala już po przeczytaniu treści widzieć sytuację.

Mila: Zrób z drutu bryłę szkieletową sześcianu, ostrosłupa to pomoże zrozumieć. Połączysz kolorowymi nitkami odpowiednie punkty i zobaczysz wszystko. W szkole przecież takie pomoce są. Rodzice moich uczniów zrobili mi w zakładach pracy mnóstwo pomocy w czasach, gdy trudno było kupić. Teraz są w sklepach z pomocami dla szkół piękne bryłki z pleksi i nie tylko.

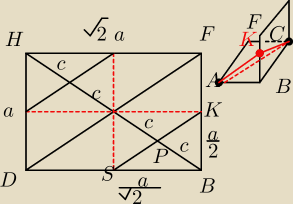
an: Jak zrozumiesz ten rysunek z : https://matematykaszkolna.pl/strona/4743.gif , tak naprawdę to opis zadania jest wystarczający i pierwszego rysunku może nie być, jak widać p/ w to tu nawet właściwie nie potrzeba nic liczyć. Nic nie kuj na pamięć bo to bezsens ulep z plasteliny sześcian możesz szpilką przebić z wierzchołka B do H otwór, a następnie odetnij narożnik B zgodnie z zadaniem jeżeli to nie wystarczy do zrumienia to zrób drugi taki podobny sześcian i przebij otwór jak poprzednio a następnie przetnij go po przekątnej HF wzdłuż krawędzi DH i FB, pooglądaj te przekroje mam nadzieję, że uruchomisz w ten sposób swą wyobraźnię przestrzenną . Następnie weź kartkę z zeszytu zgiętą w połowie rysunek z boku Patrz na te pocięte "plasteliny" i próbuj odnaleźć te płaszczyzny na tym kartkowym modelu, po kilku takich "prezentacjach" będziesz to widział w głowie, taki model możesz wykorzystać z otrzymanych kartek na maturze

Ateusz: bede kombinowal dzieki wszystkim

Mila: Tu masz inaczej rozwiązane: https://matematykaszkolna.pl/forum/353381.html

Mila: