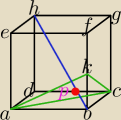
 Dany jest sześcian ABCDEFGH. Przez wierzchołki A i C oraz środek K krawędzi BF poprowadzono
płaszczyznę, która przecina przekątną BH w punkcie P.
Wykaż, że |BP|/|HP|=1/3
Dany jest sześcian ABCDEFGH. Przez wierzchołki A i C oraz środek K krawędzi BF poprowadzono
płaszczyznę, która przecina przekątną BH w punkcie P.
Wykaż, że |BP|/|HP|=1/3
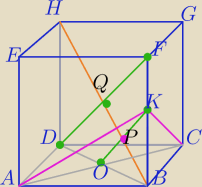 |BH|=|DF| przekątne sześcianu
OK ||DF jako odcinek łączący środki boków ΔDFB, ponadto
|BH|=|DF| przekątne sześcianu
OK ||DF jako odcinek łączący środki boków ΔDFB, ponadto
| 1 | ||
|OK|= | |DF| | |
| 2 |
| 1 | ||
ΔBOK∼ΔBDF w skali k= | ⇒ | |
| 2 |
| 1 | 1 | |||
|BP|= | |BQ|= | |BH| | ||
| 2 | 4 |
| 3 | ||
w takim razie : |HP|= | |BH|⇔ | |
| 4 |
| |BP| |
| 1 | |||||||||
= | = | ||||||||||
| |HP| |
| 3 |