Równanie prostej Magda: Napisz w postaci kierunkowej równanie prostej zawierającej dwusieczną kąta ostrego wyznaczonego przez proste o równaniach k: y=0 oraz l: y=x Bardzo proszę o wytłumaczenie!

a7: https://matematykaszkolna.pl/forum/319777.html

Magda: Widziałam właśnie, ale niestety nie rozumiem tego Skąd tam się wzięło tg22,5?

Magda: A dobrze, już wiem skąd się wzięło to 22,5, tylko nie rozumiem jak z tego wyszło √2 − 1

a7: no właśnie też nie wiem, ale umiem zrobić inną metodą tylko dłuższą

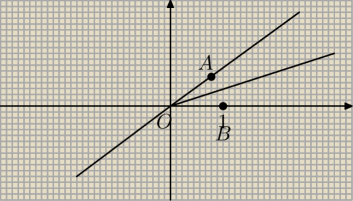
a7: przyjmujemy odcinek OA o długości 1, punkt A ma dwie te same współrzędne (x,x) , gdyż leży na prostej y=x liczymy te wspólrzedne z wzoru na dlugość odcinka i wychodzi (U{√2{2}},U{√2{2}}) nstępnie liczymy środek odcinka AB S(√2+2, √2+2)) nasza dwusieczna ma wzór y=ax+b b równe zero, gdyż przechodzi przez początek układu wspólrzędnych √2+2=a*√2+2 i stąd wychodzi a=√2−1

a7: coś źle policzyłam

a7: ale metoda jest chyba dobra

a7: S=((√2+2)/4 , √2/4 ) y=ax+b, b=0, gdyż prosta ta przchodzi przez poczatek układu wsp. ^√2₄= ^√2+2₄*a a=√2−1 teraz dobrze

Mariusz: Magda wybierasz na prostej l punkt i rzutujesz go na oś X Otrzymujesz w ten sposób trójkąt OPP' Jak już będziesz mieć trójkąt OPP' to porównujesz definicję tangensa z współczynnikiem kierunkowym otrzymanym na podstawie danych dwóch punktów Okazuje się że tangens kąta nachylenia prostej l do osi OX będzie współczynnikiem kierunkowym prostej l

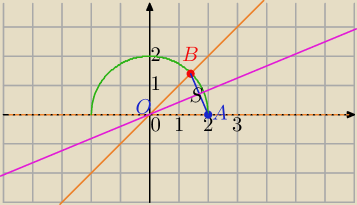
Mila: II sposób 1) Prosta y=x Obieram punkt A=(2,0) na dolnym ramieniu kąta . 2) Kreślę okrąg o środku (0,0) i r=2 Równanie okręgu: x²+y²=4 Punkt przecięcia z drugim ramieniem −B x²+x²=4, x>0 2x²=4 x²=2 x=√2, y=√2 B=(√2,√2) 3) ΔABO− Δrównoramienny Środek AB:

	√2+2		√2+0		√2+2		√2
S=(		,		)=(		,		)
	2		2		2		2

4)Prosta przechodząca przez punkty: (0,0) i S jest dwusieczną kąta AOB

	√2		√2+2
y=ax,		=a*
	2		2

√2=a*(√2+2) /*(√2−2) √2*(√2−2)=a*(2−4) a=√2−1 y=(√2−1)x

PW: Skorzystać z wzoru

	2tgα
tg2α=		;
	1−tg2α

dla α=22,5° mamy

	2tgα
tg45° =
	1−tg2α

Podstawiając dla krótkości zapisu t=tgα dostajemy równanie

	2t
1 =		,
	1−t2

z którego łatwo wyliczamy t>0.