ostro Ateusz: Podstawą ostrosłupa ABCDS jest prostokąt ABCD , w którym |AB | = 1 , |BC | = √2 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.

	−5
Wyszło mi cos=
	4√3

	−√3
A powinno wyjść
	3

Bleee: Pokaż swoje obliczenia. Nie zapomnij o rysunku

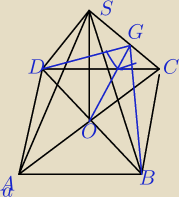Ateusz: AB=1 BC=√2 z tw Pitagorasa AC=DB=√3

	1
Z tego samego twierdzenia H=
	2

BG=? BG= wysokość BCS ΔBCS − równoramienny Przyrównanie pól :

	1
P(BCS)=
	2

P=1/2BG*CS=√1{2} BG=1 Jedno ramię już mamy, teraz drugie : ΔDCS − równoboczny

	√3
zatem wysokość DG=
	2

Z tw cosinusów : DB²=DG²+BG²−2DG*BG*cosα

	3
3=		+{1}−√3*cosα
	4

	−5		5√3
cosα=		=
	4√3		12

wredulus_pospolitus:

	1		1		√2		√6
Dlaczego P(BCS) =		? Jak dla mnie to P(BCS) =		*		*√3 =
	2		2		2		4

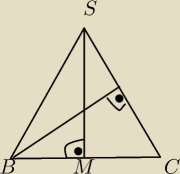Ateusz: BC=√2 BS=1 SM=h z tw pitagorasa SM²=BS²−{BM}²

	2
SM2=1−
	4

	1
SM2=
	2

	√2
SM=
	2

	1		√2		√2		1
Zatem P=		*BC*SM=		*		=
	2		2		2		2

wredulus_pospolitus: Fakt ... źle spojrzałem ... myślałem że |BC| = √3

Ateusz: Co więc jest źle

Ateusz: Pomocy.

wredulus_pospolitus: nie widze błędu

Ateusz: https://imgur.com/a/gEJrwoW Znalazłem coś takiego, jednak dalej nie mam pojęcia, dlaczego podstawą trójkąta szukanego kąta jest jakieś GD zamiast normalnie przekątnej BD Przecież kąt dwuścienny, to kąt między wysokościami dwóch ścian, a odcinek GF nie ma ani początku, ani końca w żadnym wierzchołku? O co tu chodzi?

wredulus_pospolitus: Wychodzi na to, że wysokość trójkąta BCS opuszczona z B nie 'ląduje' tam gdzie wysokośc trójkąta CDS opuszczona z D

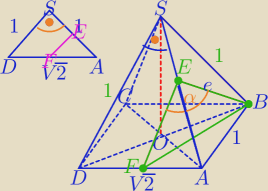Mila: 1) ΔDAS− Δprostokątny, ΔABS− Δrównoboczny DS⊥SA, 2) Musimy przesunąć równolegle DS jak na rysunku. E− środek SA FE⊥SA, BE⊥SA

	1
|EF|=
	2

	√3
e=
	2

	√2		3
|FB|2=(		)2+12=
	2		2

3) W ΔFBE:

3		1		√3		1		√3
	=(		)2+(		)2−2*		*		*cosα
2		2		2		2		2

3		√3
	=1−		*cosα
2		2

1		√3
	=−		*cosα
2		2

1=−√3*cosα

	√3
cosα=−
	3

============

Mila: Tu tłumaczyłam dlaczego tak jest , dla ogólnego przypadku z prostokątem w podstawie. Tylko tam nie zauważyłam, że kąt DSA jest prosty. https://matematykaszkolna.pl/forum/387310.html

Ateusz: Nadal nie mam pojęcia o co tu chodzi Mogłabyś narysować to jakoś na oddzielnym rysunku trójkąta, te wszystkie przesunięte wysokości danego trójkąta itp?

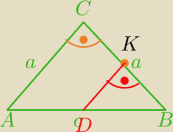Mila: K− środek BC Prowadzisz prostą równoległą do AC przechodzącą przez środek BC, czyli punkt K. DK||AC D i K − punkty łączące środki boków Δ⇔

	1
|DK|=		|AC|
	2

Ateusz: dzięki, zrozumiałe Czyli takie przesuwanie wysokości będzie zawsze, gdy będę wyznaczał kąt między pewnymi dwiema sąsiednimi ścianami bocznymi z których przynajmniej jedna jest trójkątem prostokątnym, którego kąt prosty znajduje się w kącie płaskim przy wierzchołku ostrosłupa ?

Mila: Jeżeli chodzi kąt dwuścienny, to tak. Wszystko zależy od treści zadania.