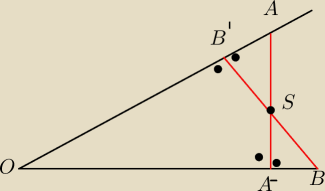
Kąt i dwusieczna 6latek: na rysunku mamy OA=OB AA'⊥OB i BB'⊥OA Wykaz ze punkt przeciecia sie odcinkow AA'i BB' nalezy do dwusiecznej kąta AOB Wobec tego musimy wykazac przystawanie trojkatow A'BS i B'AS sa to trojkaty prostokatne napewno jest A'B= B'A kąt B'SA= katowi A'SB mam juz przystawanie tych trojkatow Wedlug mnie juz moge wysnuc wniosek ze proste te przecinaja sie w polowie Wobec tego OS jest dwusieczna kąta AOB

iteRacj@: Musisz wykazać, że |A'B|=|B'A|. skorzystaj z tego, że ΔOAA' i ΔOBB' są przystające.

6latek: Wlasnie skorzystalem ale nie napisalem spojrz prosze tutaj tez https://matematykaszkolna.pl/forum/387454.html

ite: jeszcze bym napisała: dalej ΔSBA' i ΔSAB' są przystające (kbk) stąd |SB'|=|SA'| skoro odległość pkt S od obu ramion kąta jest jednakowa to należy on do dwusiecznej

6latek: dzien dobry ite Spojrz na ten moj link wyzej prosze