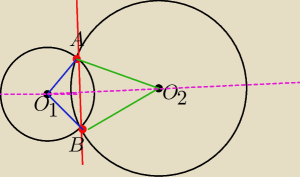
Dwa okregi 6latek: OKregi o(O₁,r₁) i o(O₂,r₂) maja wspolna cieciwe AB i r₁<r₂ wykaz ze ∡O₁AB<∡O₂AB

wredulus_pospolitus: Tw. cosinusów

wredulus_pospolitus: |AB|² = 2r₁²(1 − cos(∡AO₁B)) = 2r₂²(1 − cos(∡AO₂B)) więc: 1 − cos(∡AO₁B) > 1 − cos(∡AO₂B) i ciągniesz dalej

wredulus_pospolitus: PS. Chyba w treści zadania zrobiłeś błąd

6latek: Taka jest tresc . mam na razie dwa do przemyslenia dzieki za to i za tamto poprzednie

wredulus_pospolitus: Już z rysunku widać, że kąt przy O₁ (mniejszy okrąg) musi być większy niż przy O₂

6latek: A nie mozna na razie bez tw cosinusow ? Bo z rysunku widac ze ΔO₁ AB i ΔO₂AB to trojkaty rownoramienne kąt AO₁B >AO₂B wiec kat przy podstawie ΔO₂AB jest wiekszy

wredulus_pospolitus: Oczywiście, że możesz wykazać taką zależność kątów korzystając z trójkąta równoramiennego ... ale i tak, cosinusa najlepiej do akcji zabrać (nie musi być tw. cosinusów)

6latek: Jeszcze moze sie ktos wypowie na ten temat

ite: Widzę to tak samo jak wredulus 19:58.

	1/2*AB
cos<O1AB=
	O1A

	1/2*AB
cos<O2AB=
	O2A

liczniki obu ułamków równe, a mianowniki z zał. O₁A<O₂A I tak jak napisał w sąsiednim wątku Mariusz w trójkącie na płaszczyźnie ten kąt jest większy, którego cosinus jest mniejszy. Sposób bez cosinusów nie przychodzi mi do głowy.

6latek: dziekuje CI na razie Tylko wiesz ja tego nie rozumiem co napisal wredulus jaki trojkat wzial pod uwage? dlaczego tak a nie inaczej to napisal ? jak to pozniej pociagnac dalej ?

wredulus_pospolitus: Można np. tak: 1) Trójkąty ABO₁ i ABO₂ są równoramienne 2) Więc trójkąty ASO₁ i ASO₂ (gdzie S to środek AB) są prostokątne w takim razie:

	|AS|
sin(∡AO1S) =		−> |AS| = r*sin(∡AO1S)
	r

	|AS|
sin(∡AO2S) =		−> |AS| = R*sin(∡AO2S)
	R

więc:

	r		sin(∡AO2S)
r*sin(∡AO1S) = R*sin(∡AO2S) ⇔		=
	R		sin(∡AO1S)

wiemy, że r< R ... więc sin(∡AO₂S) < sin(∡AO₁S) więc ∡AO₂S < ∡AO₁S Natomiast kąt ∡AO₂S to nic innego niż połowa kąta ∡AO₂B, co wynika z trójkąta równoramiennego

6latek: Witaj A to tw cosinusow wytlumaczysz ? Nie spieszy sie .Mozesz pozniej .Dziekuje .

wredulus_pospolitus: tw. cosinusów. w ΔO₁AB: |AB|² = |O₁A|² + |O₁B|² − 2|O₁A|*|O₁B|*cos(∡AO₁B) czyli: |AB|² = r² + r² − 2*r*r*cos(∡AO₁B) = 2r² − 2r²*cos(∡AO₁B) = 2r²(1 − cos(∡AO₁B)) analogicznie dla drugiego trójkąta (ABO₂) więc mamy: 2r²(1 − cos(∡AO₁B)) = |AB|² = 2R²(1 − cos(∡AO₂B)) więc: r²(1 − cos(∡AO₁B)) = R²(1 − cos(∡AO₁B)) skoro r < R ... to aby zachowana była równość musi zachodzić: 1 − cos(∡AO₁B) > 1 − cos(∡AO₂B) w takim razie: cos(∡AO₂B) > cos(∡AO₁B) funkcja cosinus jest malejąca w przedziale (0,π) więc: ∡AO₂B < ∡AO₁B

6latek: Bardzo wielkie dzieki Twoja pomoc jest nieoceniona