ostro Ateusz: ostroslup W niektórych zadaniach, w ich poleceniu, nie ma żadnej informacji czy np. ściany boczne ostrosłupa są nachylone pod tym samym kątem, czy ostrosłup jest prosty (ma wszystkie krawędzie boczne równe). Co wtedy należy zrobić rysując tego ostrosłupa? Skąd mam wiedzieć gdzie będziel leżał spodek wysokości?

Mila: Jaką masz treść tego zadania?

Ateusz: np : W ostroslupie prawidlowym trojkatnym kat miedzy dwiema sasiednimi scianami bocznymi ma miare 2alfa. przez krawedz podstawy popropwadzono plaszczyzne prostopadla do przeciwleglej rkawedzi bocznej ostroslupa. wykaz, ze tworzy ona z plaszczyzna podstawy taki kat beta, ze √3tgalfacosbeta=1

Ateusz: albo podstawa ostroslupa abcdw jest prostokat abcd w ktorym ab = a bc = b. sciany boczne WAB i WDC nachylone sa do plaszczyzny podstawy pod katem alfa. wyznacz tg beta, gdzie beta to kat, pod jakim sa nachylone do plaszczyzny podstawy pozostasle dwie sciany boczne

Ateusz: hm?

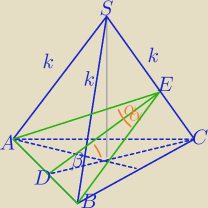
Mila: 17:58. Spodek wysokości w środku okręgu wpisanego ( opisanego) na podstawie, która jest Δrównobocznym. Krawędzie boczne równe. DE⊥SC, BE⊥SC Policzysz teraz? Łatwe.

Ateusz: @Mila zrobiłem to zadanie, bo założyłem z góry, bezpodstawnie, że spodkiem wysokości ostrosłupa będzie środek okręgu opisanego (wpisanego) w podstawę główne pytanie − na podstawie czego twierdzisz, że krawędzie boczne są równe?

Mila: Ostrosłup prawidłowy− definicja. https://matematyka.wiki/ostroslup-prawidlowy-trojkatny

Mila: Możesz zresztą obliczyć długości krawędzi. W każdym przypadku : O− spodek wysokości H k²=h²+R²

Mila: Czy do zadania z 18:00 masz odpowiedź , to napisz.

Mila: Czegoś mi brakuje w tej treści.

Mila: k²=H²+R²

Ateusz: wlasnie, co z zadaniem 18:00? tam nie mam nic prawidlowego a tu takze z gory zalozylem, ze spodek bedzie w srodku okregu opisanego

	b*tgalfa
wyszlo mi, ze tgbeta=
	a

Mila: Jaka jest odpowiedź do zadania?

Mila: Greckie literki masz w pasku nad polem tekstowym.

Ateusz: @Mila właśnie taka, greckie literki mam tylko ułamek sekundy po odświeżeniu, po czym znikają. to jak z tym 2 zadankiem, czemu tam będzie spodek w środku okręgu?

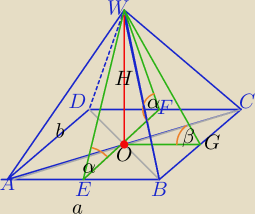
Mila: Z treści zadania : ΔEFW− Δrównoramienny ( kąty przy podstawie równe) Spodek wysokości leży w środku EF.

	b
tgβ=		tgα
	a

Ateusz: @Mila czyli po prostu celnie strzelilem w ciemno... dzieki juz wszystko wiem, wniosek nasuwa mi sie taki − jesli nie mam podane w poleceniu, czy sciany maja ten sam kat nachylenia, czy jest to ostroslup prosty, prawidlowy itp. to lokalizacja spodka wysokosci będzie musiala wynikac z reszty polecenia zajrzyj jeszcze tutaj jesli mozesz https://matematykaszkolna.pl/forum/387407.html

Mila: Nie strzelaj tylko myśl. Korzystaj z definicji i treści zadania.