tra
Ateusz: Sześcian o krawędzi a przecięto płaszczyzną zawierającą przekątną jednej ze ścian sześcianu i
nachyloną do tej ściany pod kątem alfa. Wyraź pole otrzymanego przekroju jako funkcję kąta
alfa.
Wiem, że będą dwa przypadki − przekrojem może być trójkąt równoramienny oraz trapez
równoramienny.
Z tym pierwszym przypadkiem sobie poradziłem, jednak z drugim mam problem.
| | a | |
Wyznaczyłem h= |
| , dłuższa podstawa to przekątna kwadratu, jednak z tą drugą podstawą |
| | sinalfa | |
trapezu mam problem.
Mila:
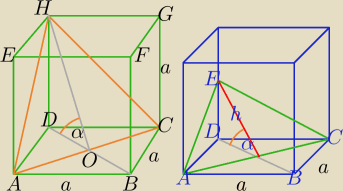
1) Sprawdzamy dla jakich α przekrój jest Δrównoramiennym.
α
0≈54.8
o
Dla α∊(0,α
0> przekrój jest Δrównoramiennym
2)α=90
o− przekrój jest prostokątem (a
√2 x a)
3) α∊(α
0, 90) przekrój jest trapezem równoramiennym
w drugim wątku
 1) Sprawdzamy dla jakich α przekrój jest Δrównoramiennym.
1) Sprawdzamy dla jakich α przekrój jest Δrównoramiennym.
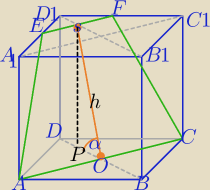 1) W ΔOPS:
1) W ΔOPS: