równanie obrazu Marek: Znajdź równanie obrazu: prostej 𝑥 − 2𝑦 + 4 w jednokładności o środku 𝑆(2,1) i skali 𝑘 = 2

iteRacj@: tak samo jak 387162

PW: Popraw równanie prostej. Wiadomo, że obrazem prostej w jednokładności jest prosta do niej równoległa. Odpowiedź jest więc łatwa − szukana prosta ma równanie ... I tylko jeden szczegół, żeby znaleźć niewiadomy "wyraz wolny" trzeba znaleźć obraz jednego z punktów prostej (sami go sobie wybieramy).

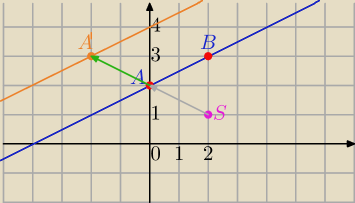
Mila: 𝑆(2,1) − środek jednokładności k=2− skala jednokładności prosta : x−2y+4=0 ⇔? 1)

	1
k: y=		x +2 punkty wykresu A=(0,2), B=(2,3)
	2

Po przekształceniu przez jednokładność otrzymujesz prostą równoległą do danej

	1
(*) k': y=		x+b
	2

2) Przekształcamy punkt A(0,2) A'=(x',y') SA'→=^df2*SA^→ SA'^→=[x'−2,y'−1], SA^→=[−2,1] [x'−2,y'−1]=2*[−2,1] x'−2=−4 i y'−1=2 x'=−2, y'=3 A'=(−2,3) 3) Podstawiamy do (*)

	1
3=		*(−2)+b, b=4
	2

	1
k' : y=		x+4
	2

============