prawdopodobieństwo vvool: Na ile sposobów można wybrać trzy wierzchołki 14−kąta foremnego, by były one wierzchołkami trójkąta prostokątnego?

Eta: 7*12 = 84 trójkąty prostokątne

vvool: mógłbym prosić o uzasadnienie?

Pytający: Żeby wybrane 3 wierzchołki tworzyły trójkąt prostokątny, 2 wierzchołki muszą "leżeć" naprzeciwko siebie (wtedy łączysz je średnicą i masz kąt środkowy 180°, a zatem kąt przy dowolnie wybranym trzecim wierzchołku jest prosty; 465).

	14
Czyli może te 3 wierzchołki wybrać na		*(14−2)=84 sposoby.
	2

vvool: dziękuje

Adamm: α = 1080/7^o kąty które trzeba odjąć (180^o−α)/2 (360^o−2α)/2 ... (180^o*14−14α)/2 sprawdźmy dla jakich 2 kątów mamy kąt prosty α = (180^o*k−kα)/2+90^o+(180^o*m−mα)/2 k+m = 5 więc mamy 6 różnych przypadków to daje w sumie 14*6 = 84 możliwości

Adamm: @Pytający no tak, trzeba było ze średnicy skorzystać

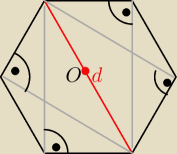
Eta: 14 −− kąt ma 7 średnic (w okręgu opisanym na nim na każdej średnicy można zbudować 14−2 =12 trójkątów prostokatnych zatem jest ich 7*12 = 84

	n
n−− parzysta liczba wierzchołków		−− liczba średnic
	2

n−2 −− liczba zbudowanych trójkątów prostokątnych na każdej średnicy

	n
to mamy:		(n−2) −−− trójkątów prostokątnych
	2

na rys. podałam dla sześciokąta foremnego 3 średnice i 4 trójkąty z każdej to razem 3*4 =12 trójkątów prostokątnych

Eta: Zanim narysowałam .... to już mnie wyprzedzili

vvool: niesamowici jesteście