| 2 | ||
co mi do głowy przychodzi to : | h=IASI | |
| 3 |

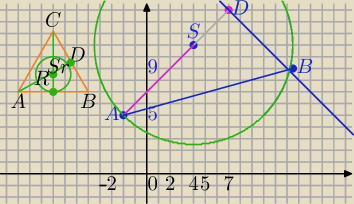 A=(−2,5), S=(4,11)
ΔABC− Δrównoboczny.
Środki okręgu wpisanego i opisanego znajdują się w tym samym punkcie.
R=|AS|=√62+62=6√2
r=3√2
1)
AS→=[6,6]
SD→=[3,3]
S=(4,11)→T[3,3]⇒D=(4+3,11+3)=(7,14)− środek boku BC
2) prosta AD:
y=x+b
BC⊥AD
prosta BC: y=−x+b i D=(7,14)∊BC
b=21
y=−x+21
3) Okrąg o środku S (4,11) i R=6√2
(x−4)2+(y−11)2=(6√2)2
(x−4)2+(y−11)2=72
Przecięcie okręgu z prostą BC⇒B i C
(x−4)2+(−x+21−11)2=72
(x−4)2+(−x+10)2=72
x1=7−3√3 lub x2=7+√3
y1=−7+3√3+21 lub y2=−7−3√3+21
y1=14+3√3 lub y2=14−3√3
B=(7+3√3, 14−3√3) i C=(7−3√3,14+3√3
================================
Posprawdzaj rachunki
A=(−2,5), S=(4,11)
ΔABC− Δrównoboczny.
Środki okręgu wpisanego i opisanego znajdują się w tym samym punkcie.
R=|AS|=√62+62=6√2
r=3√2
1)
AS→=[6,6]
SD→=[3,3]
S=(4,11)→T[3,3]⇒D=(4+3,11+3)=(7,14)− środek boku BC
2) prosta AD:
y=x+b
BC⊥AD
prosta BC: y=−x+b i D=(7,14)∊BC
b=21
y=−x+21
3) Okrąg o środku S (4,11) i R=6√2
(x−4)2+(y−11)2=(6√2)2
(x−4)2+(y−11)2=72
Przecięcie okręgu z prostą BC⇒B i C
(x−4)2+(−x+21−11)2=72
(x−4)2+(−x+10)2=72
x1=7−3√3 lub x2=7+√3
y1=−7+3√3+21 lub y2=−7−3√3+21
y1=14+3√3 lub y2=14−3√3
B=(7+3√3, 14−3√3) i C=(7−3√3,14+3√3
================================
Posprawdzaj rachunki

