Trojkat 6latek: Dany jest trojkata ABC i punkt D rozny od A i B ze punkt A lezy pomiedzy B i D Jakim rodzajem jest dany trokat jesli dwusieczna kąta DAC i wysokosc porowadzona z wierzcholka A sa prostopadle

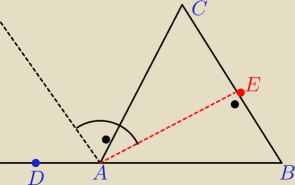
6latek: To taki rysunek musialby byc do zadania

lizinczyk: to nie to samo? https://matematykaszkolna.pl/forum/371365.html

6latek: fajnie . to samo

vvool: mnie zastanawia czy wy próbujecie sami rozwiązać zadanie czy najpierw w necie szukacie rozwiązania albo pamiętacie tak te zadania

6latek: I tak bede musial dopytac ale to jak wroce ze spaceru Bedzie swiezszy mozg

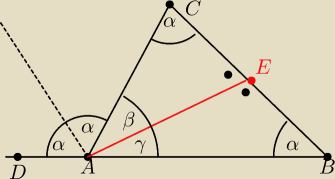
6latek: Milu Mam pytania do Ciebie co do tego zadania bo nie ma Basi na forum nr 1. Kąt ABC α to wiadomo nr 2 Dlaczego kąt BCA tez jest oznaczony przez α? Czyzby twierdzenie o rownych kątach o raminach odpowiednio prostopadlych ? Jesli tak to ktore te ramiona ? Nr 3 Dlaczego Basia oznaczyla kąty przy dwusiecznej tez przez α. Wedlug mnie to blad bo nie wiemy przeciez czy dwusieczna jest rownolegla do BC dziekuje za odpowiedz

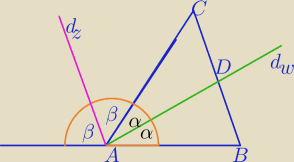
Mila: Dwusieczna kąta zewnętrznego jest prostopadła do dwusiecznej przyległego kąta wewnętrznego. Dwusieczne kątów przyległych są prostopadłe . 2α+2β=180^o α+β=90 Jeżeli AD jest wysokością to Δ musi b równoramienny: AB≡AC, wtedy wysokość jest dwusieczną .

6latek: Milu Ale na poczatku nie wiemy ze wysokosc AD jest dwusieczna d_w

6latek:

Mila: Już patrzę , nie widziałam Twojego wpisu 18:42, gdy pisałam. Podałam ogólne wiadomości.

Mila: Oznaczenia wprowadziła dla kąta zewnętrznego. Wysokość jest dwusieczną kąta w Δ równoramiennym, równobocznym.

6latek: Jeszcze bede myslal

ite: Dwusieczne kątów przyległych są prostopadłe. → dwusieczna kąta DAC ⊥ dwusieczna kąta BAC Z treści zadania: dwusieczna kąta DAC i wysokość poprowadzona z wierzchołka A są prostopadle → dwusieczna kąta BAC i wysokość poprowadzona z wierzchołka A są równoległe Pkt A jest ich punktem wspólnym → dwusieczna kąta BAC i wysokość poprowadzona z wierzchołka A pokrywają się oraz |<CAE|=<|BAE| (dzieli dwusieczna) , <CEA|=<|BEA|=90^o , AE bok wspólny → ΔACE≡ΔABE (kbk) więc ΔABC jest równoramienny

6latek: Dzien dobry No to zaszalas . ja wlasnie wstalem

ite: Dzień dobry 18:42 Nr 3 Basia przyjęła, że miara <DAC=2α, bo łatwiej jest zapisywać połówki kątów, a to jest potrzebne przy rysowaniu dwusiecznej. Nr 2 Dlaczego kąt BCA też jest oznaczony przez α? To wynika z tego, że ΔACE jest prostokątny.

6latek: Zamowilem sobie ksiazke i pojade wplacic kase za nia Jak wroce to sobie obroce ten trojkat ABC i zobacze czy nie da sie zastosowac tego twierdzenia o ramionach odpowiednio prostopadlych