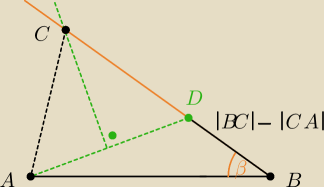
elementarne konstrukcyjne geometryczne iteRacj@: To jest zadanie 69 z podręcznika z wątku 386618. Zakładam nowy wątek, bo tam tłoczno. Wymyśliłam taką konstrukcję, czy jest poprawna? Skonstruuj trójkąt ABC, mając dane: odcinek s=|BC|−|CA|, bok AB i kąt <ABC=β. rysuję odcinek AB i kąt <ABC=β na ramieniu kąta zaznaczam odcinek s=|BC|−|CA|, otrzymuję pkt D łączę A i D odcinkiem znajduję jego symetralną punkt przecięcia symetralnej z ramieniem kąta β jest trzecim wierzchołkiem trójkąta ?

6latek: O ktorej bedziesz rano na forum?

iteRacj@: Sugerujesz, że może rano wymyślę coś lepszego ? Chyba nie... Ale zadania mi się spodobały, wymagają uruchomienia wyobraźni. Jutro cały dzień nie będę mieć dostępu do internetu.

6latek: Nie . szkoda ze Cie nie bedzie . Teraz slucham audycji z pulkownikiem Wronskim . Do zobaczenia na forum pojutrze

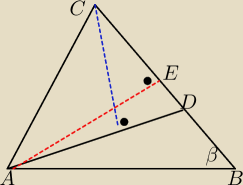
6latek: Twoje rozwiazanie jest dobre wedlug autorki dalej piszse tak Z tresci zadania wynika ze BC>CA a wiec kat CAB > kata ABC Jesli zatem β≥90^o to zadanie nie ma rozwiazania Zalozmy teraz z e β jest ostry i oznaczmy przez E rzut prostokatny punktu A na prosta BD Jesli s <BE to zadanie ma jedno rozwiazanie W przeciwnym wypadku nie ma rozwiazan

ite: To teraz już wiem, jak w tym zadaniu powinien wyglądać dowód poprawności konstrukcji.

6latek: Na jednym ramieniu kata β odkladamy od wierzcholka B odcinek |BA| na drugim odcinek o dlugosci s Otrzymujemujemy w ten sposob punkty A i D . Punkt przeciecia symetralnej odcinka AD z polprosta BD jest wierzcholkiem C trojkata Tyle w rozwiazaniu